
Если а(t) – непрерывная функция, то
(а(t) d(t), j(t)) = (d(t), а(t) j(t)) = a(o) j(o) (j Î Ko).
Отметим, что функционал f, определенный на K соотношением

не является обобщенной функцией, так как, являясь непрерывным функционалом, он не линеен.
3. Обобщенная функция Хевисайда
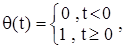
для которой можно записать

является регулярной обобщенной функцией.
Действия над обобщенными функциями
Введем в пространстве обобщенных функций K' операцию предельного перехода. Последовательность  сходится к f, если для любого j Î K выполнено следующее соотношение
сходится к f, если для любого j Î K выполнено следующее соотношение
(fn, j) ® (f, j)
n ®¥
Определим теперь для обобщенных функций операцию дифференцирования и рассмотрим ее свойства. Производная f '(t) регулярной обобщенной функции f (t) равна

так как основная функция обращается в нуль вне некоторого конечного интервала. Производная n – го порядка будет тогда определяться равенством
(f(n) (t), j(t) = (-1)n (f (t), j(n) (t)) (" n Î N, j Î K).
Это соотношение определяет производную n – го порядка обобщенных функций, включая и сингулярные функции.
Примеры:
1. Производная функции Хевисайда равна
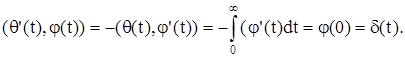
2. Так как

то

Из определения дельта – функции следует
t d(t) = 0,
а значит
d(t) + t d'(t) = 0,
2d'(t) + t d''(t) = 0,
---------------------
nd(n-1)(t) + t d(n)(t) = 0.
Отсюда последовательным исключением получаем
tn d(n) (t) = (-1) n! d(t) n Î N.
Методом математической индукции можно показать, что

Легко также показать, что если a(t) Î Cm, то
a(t) d(m) (t – to) = Com a (to) d(m) (t – to) - C1m a' (to) d(m-1) (t – to) –
-... – (-1)Cmm a(m) (to) d (t – to).
Введем обобщенные функции t + и t -:

тогда
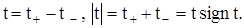
Можно вычислить производные
(t+)' = q(t), (t-)' = -q(-t),
а также
n 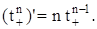
 2020-04-20
2020-04-20 173
173








