Вище згадувалося про існування аналітичних форм представлення булевих ф-цій. Тут розглянемо універсальні (канонічні) форми представлення, які дають можливість отримати аналітичну форму безпосередньо по таблиці істиності для довільної булевої ф-ції. Ця форма в дальшому може бути спрощена. Найбільш широке поширення отримала досконала нормальна форма (ДНФ). Перед тим як перейти до вивчення, приведемо визначення конституєнти одиниці - поняття, яким будемо широко користуватися дальше.
Визначення: Конституєнтою одиниці називається функція f (x1, x2, …, xn), яка приймає значення 1 тільки на одному наборі.
Якщо згадати, що диз’юнкція рівна 1, коли хоча б одна з змінних приймає значення 1, то можна легко виразити, будь-яку булеву функцію як диз’юнкцію конституєнт одиниці, які відповідають тим наборам, на яких функція рівна 1. В більш загальному вигляді це можна записати таким чином:
f (x1, x2, …, xn) = 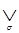 f (σ1, σ2, …, σn) * x1 σ1, x2 σ2, …, xn σn,
f (σ1, σ2, …, σn) * x1 σ1, x2 σ2, …, xn σn,
де σi = 0,1 і
xi σi = 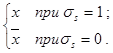
Ця форма і є досконала диз’юнктивна форма (ДДНФ). Замітимо, що набори, де функція f приймає значення 1, часто називають одиничними, всі решта - нульовими наборами. Виписувати в ДДНФ є зміст тільки конституєнти одиниці, відповідні одиничним наборам.
Приклад: Випишемо ДДНФ для ф-цій, заданих таблицею істиності (табл.1).
Таблиця 1
| x1 x2 x3 | f1 | f2 |
| 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 | 0 1 1 0 1 0 0 1 | 0 0 0 1 0 1 1 1 |
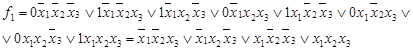
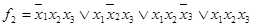
Ф-ція f1 нам відома як сума за модулем 2 трьох змінних х1 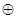 х2
х2 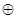 х3. Ф-ція f2 називається мажорантною (вона приймає значення, яке приймає більшість змінних) і позначається знаком М (х1, х2, х3)
х3. Ф-ція f2 називається мажорантною (вона приймає значення, яке приймає більшість змінних) і позначається знаком М (х1, х2, х3)
Друга відома форма носить назву “досконалої кон’юктивної нормальної форми" (ДКНФ). Вона будується аналогічно ДДНФ.
Визначення: Конституєнтою нуля називається функція, яка приймає значення 0 на єдиному наборі.
Конституєнта нуля записується у вигляді елементарної диз’юнкції всіх змінних. Кожному набору відповідає своя конституєнта 0.
Приклад Для розглянутих вище ф-цій х1 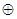 х2
х2 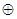 х3 і М (х1, х2, х3) (табл.7) побудуємо ДКНФ:
х3 і М (х1, х2, х3) (табл.7) побудуємо ДКНФ:
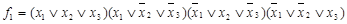 ;
;
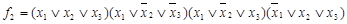 .
.
Легко побачити, що в ДДНФ можна замінити операцію диз’юнкції операцією суми за модулем 2, причому рівність збережеться. Ця форма називається “досконалою поліноміальною нормальною формою” (ДПНФ). Для нашого прикладу
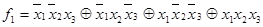
|
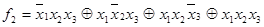
Якщо в ДПНФ замінити всі змінні з запереченням у відповідності з співвідношенням 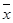 =1
=1 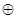 х, то отримається канонічний поліном Жегалкіна вигляду
х, то отримається канонічний поліном Жегалкіна вигляду
f (x1, x2, …, xn)
=a0 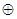 a1x1
a1x1 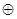 a2x2
a2x2 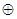 …
… 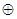 anxn
anxn 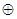 a12x1x2
a12x1x2 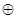 a13x13
a13x13 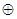 …
… 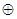 a12…nx1x2…xn,
a12…nx1x2…xn,
де аi 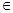 {0,1}.
{0,1}.
Приклад: Для тих же функцій f1 і f2 знайдемо канонічний поліном Жегалкіна:
f1= (x1 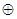 1) (x2
1) (x2 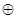 1) x3
1) x3 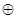 (x1
(x1 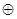 1) x2 (x3
1) x2 (x3 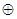 1)
1) 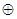 x1 (x2
x1 (x2 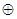 1) (x3
1) (x3 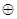 1)
1) 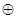 x1x2x3= x1x2x3
x1x2x3= x1x2x3 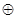 x3
x3 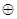 x1x3
x1x3 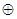 x2x3
x2x3 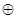
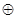 x1x2x3
x1x2x3 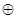 x1x2
x1x2 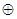 x2x3
x2x3 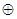 x1x2x3
x1x2x3 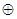 x1x2
x1x2 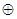 x2x3
x2x3 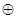 x2
x2 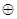 x1x2x3
x1x2x3 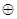 x1x2
x1x2 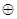 x1x3
x1x3 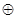 x1
x1 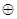 x1x2x3=x1
x1x2x3=x1 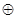 x2
x2 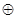 x3
x3
Аналогічно для f2= x1x2 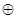 x2x3
x2x3 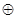 x1x3.
x1x3.
В булевій алгебрі широко використовується розклад Шеннона- формула, яка дозволяє перейти від представлення функції від n-змінних до представлення функції від (n-1) - змінних:
f (x1, x2, …, xn) =x1f (1, x2, …, xn) 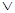
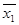 f (0, x2, …, xn)
f (0, x2, …, xn)
Співвідношення легко узагальнюється для будь-якої кількості змінних, якщо функції правої частини піддати такому ж розкладу по інших змінних. Наприклад:
f (x1, x2, …, xn) =x1 [x2f (1,1, x3, …, xn) 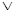
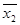 f (1,0, x3, …, xn)]
f (1,0, x3, …, xn)] 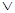
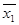 [x2f (0,1, x3…xn)
[x2f (0,1, x3…xn) 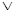
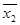 f (0,0,x3,…xn)] =x1,x2f (1,1,x3,…xn)
f (0,0,x3,…xn)] =x1,x2f (1,1,x3,…xn) 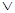 x1
x1 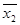 f (1,0,x3,…,xn)
f (1,0,x3,…,xn) 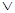
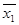 x2f (0,1,x3,..,xn)
x2f (0,1,x3,..,xn) 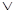
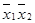 f (0,0,x3,…,xn)
f (0,0,x3,…,xn)
Відмітимо, що якщо провести такий же розклад по всіх змінних, получиться ДДНФ.
 2020-04-20
2020-04-20 145
145








