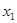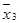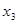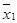Метод представляє собою формалізований на етапі знаходження простих імплікант метод Квайна. Формалізація проводиться таким чином:
Всі конституанти одиниці з ДДНФ булевої функцію f записуються їх двійковими номерами.
Всі номери розбиваються на групи, що не перетинаються. Ознака утворення і-ї групи: і одиниць в кожному двійковому номері конституєнти одиниці.
Склеювання проводять тільки між номерами сусідніх груп. Склеювані номери відмічається будь-яким знаком (закреслюванням).
Склеювання проводять всеможливі, як і в методі Квайна.
Невідмічені після склеювання номера є простими імплікантами.
Знаходження мінімальних ДНФ дальше проводяться на імплікантній матриці, як і в методі Квайна.
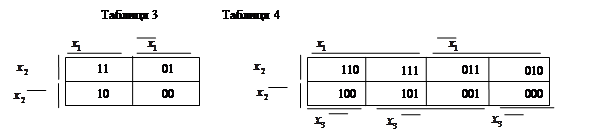
Метод дозволяє швидко отримати мінімальні ДНФ булевої функції f невеликого числа змінних. В основі методу лежить задання булевих функцій діаграмами деякого спеціального виду, які дістали назву діаграм Вейча. Для булевої ф-ції двох змінних діаграма Вейча має вигляд (табл.3) Кожна клітка діаграми відповідає набору змінних булевої функції в її таблиці істиності. В клітці діаграми ставиться одиниця, якщо булева функція приймає одиничне значення на відповідному наборі. Нульові значення булевої функції в діаграмі не ставляться. Для булевої функції трьох змінних діаграма Вейча має такий вигляд (табл.4)
Додаванням до неї ще такої ж таблиці ми отримаємо діаграму для функції 4-х змінних (табл.5). Таким же чином можна отримати діаграму 5-ти змінних і т.д.
Таблиця 5
 |  |

 1100 1100
| 1101 | 1001 | 1000 | ||||
 1110 1110
| 1111 | 1011 | 1010 | ||||
| 0111 | 0011 | 0010 | ||||
 0100 0100
| 0101 | 0001 | 0000 |
|
|
Кожній клітці діаграми відповідає свій набір.
Сусідні набори розміщені поряд в рядку або в стовбці.
Сусідніми наборами називають набори, які відрізняються однією компонентою.
Ще одне важливе зауваження: стовбці, розміщені по краях діаграми, також вважають сусідніми.
Загальне правило склеювання на діаграмі Вейча можна сформолювати таким чином: склеюванню підлягають прямокутні конфігурації, заповнені одиницями і які містять число кліток, що являються степінню 2. Отримане повне елементарне перетворення визначається як перетворення змінних, які не змінюють свого значення на всіх склеюваних наборах. Число m змінних, які залишились в елементарному перетворенні визначається легко:
m = n - log2M,
де n - число змінних функції; М - число склеюваних наборів. Метод широко використовується на практиці, завдяки простоті і зручності.
Мінімізація булевої ф-ції полягає в знаходженні мінімального накриття всіх одиниць діаграми Вейча блоками з одиниць (вказаної конфігурації), розміщених в сусідніх клітках діаграми. При цьому завжди вважають, що лівий край діаграми Вейча 4-х змінних прилягає до її правого краю, а верхній край діаграми - до її нижнього краю. Після отримання максимального покриття всіх одиниць діаграми Вейча, мінімальна ДНФ булевої функції записується як диз’юнкція елементарних кон’юнкцій, які відповідають виділеним блокам одиниць в діаграмі.
Приклад. Булева функція f має наступну ДДНФ:
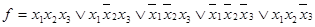
Знайти мінімальну ДНФ з допомогою діаграми Вейча. Діаграма Вейча, що відповідає функції f, представлена в табл.18. Мінімальне накриття всіх одиниць діаграми можливе тільки блокамипо дві одиниці. Кожному такому блоку відповідає своя кон’юнкція, як показано в табл.22. Отже, мінімальна ДНФ ф-ції має вигляд:
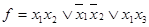 .
.
Таблиця 18
 |
Висновок
Отже, ключовими математичними поняттями теорії цифрових автоматів являється т. зв. булева алгебра та її під-дисципліни, які і визначають її математичний базис.
Література
1. А.Я. Савельев. Арифметические и логические основы цифровых автоматов. М.: Высшая школа. 1999.
2. А.Я. Савельев. Прикладная теория цифровых автоматов. М.: Высшая школа. 2007.
3. Е.Н. Вавилов, Г.П. Портной. Синтез схем электронных цифровых машин. М.: Советское радио. 2003.
4. Г.Н. Соловьев. Арифметические устройства ЭВМ. М.: Энергия. 2008.
 2020-04-20
2020-04-20 192
192