Перелік умовних позначок
У роботі всі розглянуті групи передбачаються кінцевими. Буквами 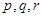 позначаються прості числа.
позначаються прості числа.
Будемо розрізняти знак включення множин  і знак строгого включення
і знак строгого включення  ;
;
 і
і 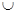 - відповідно знаки перетинання й об'єднання множин;
- відповідно знаки перетинання й об'єднання множин;
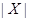 - потужність множини
- потужність множини 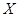 ;
;
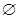 - порожня множина;
- порожня множина;
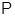 - множина всіх простих чисел;
- множина всіх простих чисел;
 - деяка множина простих чисел, тобто
- деяка множина простих чисел, тобто 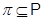 ;
;
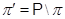 - доповнення до
- доповнення до  у множині всіх простих чисел; зокрема,
у множині всіх простих чисел; зокрема, 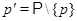 ;
;
Нехай  - група. Тоді:
- група. Тоді:
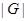 - порядок групи
- порядок групи  ;
;
 - порядок елемента
- порядок елемента  групи
групи  ;
;
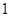 - одиничний елемент і одинична підгрупа групи
- одиничний елемент і одинична підгрупа групи  ;
;
 - множина всіх простих дільників порядку групи
- множина всіх простих дільників порядку групи  ;
;
 - множина всіх різних простих дільників натурального числа
- множина всіх різних простих дільників натурального числа  ;
;
 - група - група
- група - група  , для якої
, для якої  ;
;
 - група - група
- група - група  , для якої
, для якої 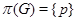 ;
;
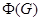 - підгрупа Фратіні групи
- підгрупа Фратіні групи  , тобто перетинання всіх максимальних підгруп
, тобто перетинання всіх максимальних підгруп  ;
;
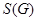 - найбільша нормальна розв'язна підгрупа групи
- найбільша нормальна розв'язна підгрупа групи  ;
;
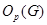 - найбільша нормальна
- найбільша нормальна  --підгрупа групи
--підгрупа групи  ;
;
 - найбільша нормальна
- найбільша нормальна  --підгрупа групи
--підгрупа групи  ;
;
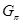 -
-  --холовська підгрупа групи
--холовська підгрупа групи  ;
;
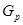 - силовська
- силовська  --підгрупа групи
--підгрупа групи  ;
;
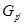 - доповнення до силовської
- доповнення до силовської  --підгрупи в групі
--підгрупи в групі  , тобто
, тобто  --холовська підгрупа групи
--холовська підгрупа групи  ;
;
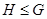 -
- 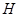 є підгрупою групи
є підгрупою групи  ;
;
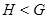 -
- 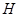 є власною підгрупою групи
є власною підгрупою групи  ;
;
 -
-  є максимальною підгрупою групи
є максимальною підгрупою групи  ;
;
 -
- 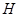 є нормальною підгрупою групи
є нормальною підгрупою групи  ;
;
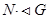 -
- 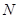 є мінімальною нормальною підгрупою групи
є мінімальною нормальною підгрупою групи  ;
;
 - індекс підгрупи
- індекс підгрупи 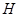 в групі
в групі  ;
;
 ;
;
 - централізатор підгрупи
- централізатор підгрупи 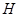 в групі
в групі  ;
;
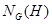 - нормалізатор підгрупи
- нормалізатор підгрупи 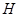 в групі
в групі  ;
;
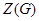 - центр групи
- центр групи  ;
;
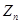 - циклічна група порядку
- циклічна група порядку  ;
;
Якщо  , то
, то  .
.
Якщо 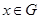 ,
,  , то
, то 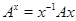 .
.
Класи груп, тобто сукупності груп, замкнуті відносно ізоморфізмов, позначаються прописними готичними буквами. За деякими класами закріплені стандартні позначення:
 - клас всіх груп;
- клас всіх груп;
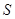 - клас всіх розв'язних груп.
- клас всіх розв'язних груп.
Основні поняття
Групою називається непуста множина  з бінарною алгебраїчною операцією (множенням), що задовольняє наступною вимогою:
з бінарною алгебраїчною операцією (множенням), що задовольняє наступною вимогою:
1) операція визначена на  , тобто
, тобто  для всіх
для всіх 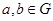 ;
;
2) операція асоціативна, тобто 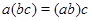 для будь-яких
для будь-яких 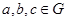 ;
;
3) в  існує одиничний елемент, тобто такий елемент
існує одиничний елемент, тобто такий елемент  , що
, що 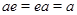 для всіх
для всіх 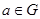 , що
, що 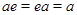 для всіх
для всіх 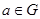 ;
;
4) кожний елемент володіє зворотним, тобто для кожного 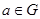 існує такий елемент
існує такий елемент 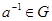 , що
, що 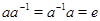 .
.
Більш коротко: напівгрупа з одиницею, у якій кожний елемент володіє зворотним, називається групою.
Групу з комутативною операцією називають комутативною або абелевої. Якщо  - кінцева множина, що є групою, то
- кінцева множина, що є групою, то  називають кінцевою групою, а число
називають кінцевою групою, а число 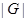 елементів в
елементів в  - порядком групи
- порядком групи  .
.
Підмножина 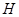 групи
групи  називається підгрупою, якщо
називається підгрупою, якщо 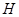 - група щодо тієї ж операції, що визначена на
- група щодо тієї ж операції, що визначена на  . Запис
. Запис 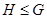 означає, що
означає, що 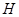 - підгрупа групи
- підгрупа групи 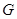 , а
, а  - що
- що 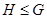 - власна підгрупа групи
- власна підгрупа групи  , тобто
, тобто 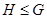 й
й  .
.
Теорема 1 Непуста підмножина 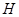 групи
групи  буде підгрупою тоді й тільки тоді, коли
буде підгрупою тоді й тільки тоді, коли 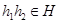 й
й  для всіх
для всіх 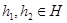 .
.
Нехай  - непуста підмножина групи
- непуста підмножина групи  . Сукупність всіх елементів групи
. Сукупність всіх елементів групи 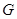 , з кожним елементом множини
, з кожним елементом множини  , називається централізатором множини
, називається централізатором множини 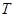 в групі
в групі 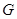 й позначається через
й позначається через  .
.
Лема 2 1. Якщо  - підмножина групи
- підмножина групи  , то централізатор
, то централізатор 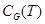 є підгрупою.
є підгрупою.
2. Якщо 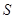 й
й  - підмножина групи
- підмножина групи  й
й 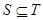 , то
, то  .
.
3. Якщо  - підмножина групи
- підмножина групи  й
й 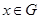 , то
, то 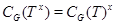 .
.
Центром групи  називається сукупність всіх елементів з
називається сукупність всіх елементів з 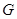 , з кожним елементом групи. Центр позначається через
, з кожним елементом групи. Центр позначається через 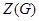 . Ясно, що
. Ясно, що 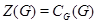 , тобто центр групи
, тобто центр групи  збігається із централізатором підмножини
збігається із централізатором підмножини  в групі
в групі 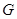 . Крім того,
. Крім того,  .
.
Зафіксуємо в групі  елемент
елемент 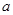 . Перетинання всіх підгруп групи
. Перетинання всіх підгруп групи 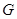 , що містять елемент
, що містять елемент 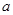 , назвемо циклічною підгрупою, породженої елементом
, назвемо циклічною підгрупою, породженої елементом 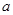 , і позначимо через
, і позначимо через 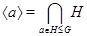 .
.
Теорема 3 Циклічна підгрупа 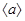 , породжена елементом
, породжена елементом 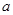 , складається із усіляких цілих ступенів елемента
, складається із усіляких цілих ступенів елемента 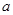 , тобто
, тобто 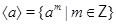 .
.
Наслідок 4 Циклічна підгрупа абелева.
Нехай 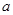 - елемент групи
- елемент групи  . Якщо всі ступені елемента
. Якщо всі ступені елемента 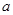 різні, тобто
різні, тобто  для всіх цілих
для всіх цілих  , то говорять, що елемента
, то говорять, що елемента 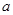 має нескінченний порядок.
має нескінченний порядок.
Якщо  - непуста підмножина групи
- непуста підмножина групи  й
й  те
те 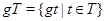 й
й  . Елемент
. Елемент  називається перестановочним з підмножиною
називається перестановочним з підмножиною 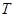 , якщо
, якщо 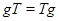 . Рівність
. Рівність 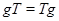 означає, що для будь-якого елемента
означає, що для будь-якого елемента 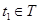 існує такий елемент
існує такий елемент 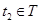 , що
, що 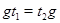 . Якщо елемент
. Якщо елемент 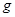 перестановочний з підмножиною
перестановочний з підмножиною  , то
, то 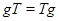 й
й 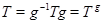 . Сукупність всіх елементів групи
. Сукупність всіх елементів групи  , перестановочних з підмножиною
, перестановочних з підмножиною 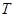 , називається нормалізатором підмножини
, називається нормалізатором підмножини  в групі
в групі  й позначається через
й позначається через 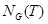 . Отже,
. Отже,
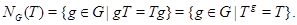
5. Нехай  - непуста підмножина групи
- непуста підмножина групи  ,
, 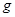 - довільний елемент групи
- довільний елемент групи 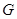 . Тоді:
. Тоді:
1)  ;
;
2)  ;
;
3) 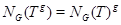 ;
;
4)  ;
;
5) якщо 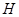 - підгрупа групи
- підгрупа групи  , те
, те 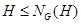 .
.
Підгрупа 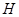 називається нормальною підгрупою групи
називається нормальною підгрупою групи 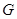 , якщо
, якщо 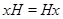 для всіх
для всіх 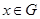 . Запис
. Запис 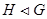 читається: "
читається: " 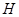 - нормальна підгрупа групи
- нормальна підгрупа групи 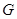 ". Рівність
". Рівність 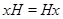 означає, що для будь-якого елемента
означає, що для будь-якого елемента 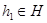 існує елемент
існує елемент 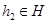 такий, що
такий, що  .
.
Теорема. 6 Для підгрупи 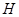 групи
групи  наступні твердження еквівалентні:
наступні твердження еквівалентні:
1) 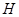 - нормальна підгрупа;
- нормальна підгрупа;
2) підгрупа 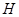 разом з кожним своїм елементом містить всі йому сполучені елементи, тобто
разом з кожним своїм елементом містить всі йому сполучені елементи, тобто 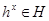 для всіх
для всіх  ;
;
3) підгрупа 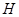 збігається з кожною своєю сполученою підгрупою, тобто
збігається з кожною своєю сполученою підгрупою, тобто 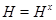 для всіх
для всіх  .
.
Нехай 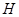 - підгрупа групи
- підгрупа групи  . Тоді:
. Тоді:
1) 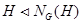 ;
;
2) якщо 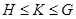 й
й 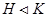 , те
, те 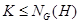 ;
;
3) 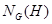 - найбільша підгрупа групи
- найбільша підгрупа групи  , у якій
, у якій 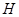 нормальна;
нормальна;
4) якщо 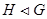 , те
, те 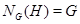 . Обернено, якщо
. Обернено, якщо 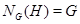 , те
, те 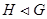 ;
;
5) 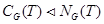 для будь-якої непустої підмножини
для будь-якої непустої підмножини  групи
групи 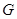 .
.
У кожній групі  тривіальні підгрупи (одинична підгрупа
тривіальні підгрупи (одинична підгрупа 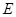 й сама група
й сама група 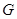 ) є нормальними підгрупами. Якщо в неодиничній групі
) є нормальними підгрупами. Якщо в неодиничній групі  немає інших нормальних підгруп, то група
немає інших нормальних підгруп, то група  називається простій. Одиничну групу
називається простій. Одиничну групу 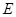 вважають непростий.
вважають непростий.
Ізометрії
Знакозмінні простори
Векторний простір  над полем
над полем 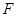 називається знакозмінним, якщо на ньому задана знакозмінна білінійна форма
називається знакозмінним, якщо на ньому задана знакозмінна білінійна форма 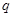 , тобто відображення
, тобто відображення 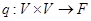 з наступними властивостями:
з наступними властивостями:


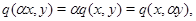
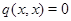
для всіх 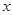 ,
, 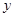 ,
, 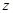 з
з  і всіх
і всіх  з
з 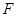 . Відзначимо наслідок цих співвідношень:
. Відзначимо наслідок цих співвідношень: 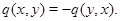 . Якщо
. Якщо 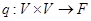 - знакозмінна форма й
- знакозмінна форма й  - довільний елемент із
- довільний елемент із 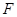 , то відображення
, то відображення 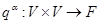 , певне формулою
, певне формулою  , і складний об'єкт, що є вихідним векторним простором
, і складний об'єкт, що є вихідним векторним простором  із цією новою формою
із цією новою формою 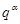 , буде знакозмінним простором, що ми позначимо через
, буде знакозмінним простором, що ми позначимо через 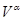 .
.
Уявлення знакозмінного простору  в знакозмінний простір
в знакозмінний простір  (обоє над полем
(обоє над полем 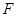 і з формами, позначуваними через
і з формами, позначуваними через 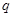 ) є по визначенню лінійне перетворення
) є по визначенню лінійне перетворення  простору
простору  в
в  , таке, що
, таке, що 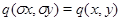 для всіх
для всіх 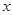 ,
,  . Інвективне уявлення називається ізометрією
. Інвективне уявлення називається ізометрією  в.
в.  Простору
Простору  й
й  називаються ізометричними, якщо існує ізометрія
називаються ізометричними, якщо існує ізометрія  на
на  . Нехай
. Нехай 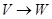 позначає уявлення,
позначає уявлення, 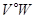 - ізометрію ``в'', а
- ізометрію ``в'', а 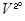 або
або 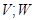 - ізометрію ``на''. Очевидно, що композиція дві ізометрії - ізометрія й перетворення, зворотне до ізометрії, - також ізометрія. Зокрема, множину ізометрій простору
- ізометрію ``на''. Очевидно, що композиція дві ізометрії - ізометрія й перетворення, зворотне до ізометрії, - також ізометрія. Зокрема, множину ізометрій простору  на себе є підгрупою загальної лінійної групи
на себе є підгрупою загальної лінійної групи 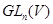 абстрактного векторного простору
абстрактного векторного простору  ; вона називається симплектичною групою знакозмінного простору
; вона називається симплектичною групою знакозмінного простору  й позначається через
й позначається через 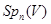 . Для будь-якого ненульового елемента
. Для будь-якого ненульового елемента 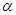 з
з 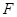 маємо
маємо  .
.
Пропозиція.7 Нехай 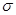 - лінійне перетворення знакозмінного простору
- лінійне перетворення знакозмінного простору  в знакозмінний простір
в знакозмінний простір  . Припустимо, що існує база
. Припустимо, що існує база 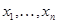 простору
простору 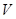 , така, що
, така, що  для всіх
для всіх  ,
, 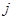 . Тоді
. Тоді 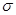 - уявлення.
- уявлення.
Доказ. Це тривіально треба з визначень.
Кожному знакозмінному простору 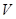 зі знакозмінною формою
зі знакозмінною формою 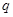 зіставимо відображення
зіставимо відображення 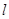 й
й  простори
простори 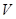 в сполучений простір
в сполучений простір  (
(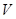 розглядається як абстрактний векторний простір над
розглядається як абстрактний векторний простір над 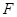 ). По визначенню відображення
). По визначенню відображення 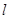 зіставляє довільному елементу
зіставляє довільному елементу 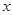 з
з 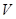 лінійний функціонал
лінійний функціонал 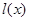 , певний формулою
, певний формулою 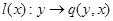 , а
, а  переводить
переводить 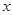 в.
в.  Легко перевіряється, що
Легко перевіряється, що  і
і  є лінійними перетвореннями.
є лінійними перетвореннями.
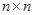 - матриця
- матриця 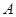 над
над 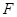 називається косо симетричною, якщо
називається косо симетричною, якщо 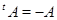 , і знакозмінної, якщо
, і знакозмінної, якщо  й на головній діагоналі коштують нулі. Таким чином, знакозмінні матриці є косо симетричними. Обернено, косо симетричні матриці є знакозмінними, якщо характеристика поля
й на головній діагоналі коштують нулі. Таким чином, знакозмінні матриці є косо симетричними. Обернено, косо симетричні матриці є знакозмінними, якщо характеристика поля 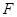 не дорівнює
не дорівнює 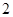 . Розглянемо знакозмінний простір
. Розглянемо знакозмінний простір 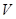 . Ми можемо асоціювати з базою
. Ми можемо асоціювати з базою 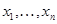 простору
простору 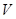 матрицю, у якої на місці
матрицю, у якої на місці  коштує
коштує 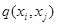 . Назвемо
. Назвемо 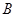 матрицею знакозмінного простору
матрицею знакозмінного простору 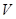 в базі
в базі 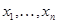 й будемо писати
й будемо писати 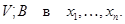
Якщо існує хоча б одна база, у якій 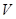 має матрицю
має матрицю 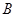 , то будемо писати
, то будемо писати 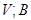 . Матриця
. Матриця 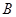 , асоційована зі знакозмінним простором
, асоційована зі знакозмінним простором 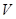 зазначеним способом, є, мабуть, знакозмінної. Що відбувається при зміні бази? Припустимо, що
зазначеним способом, є, мабуть, знакозмінної. Що відбувається при зміні бази? Припустимо, що  в базі
в базі  й
й 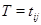 - матриця переходу від першої бази до другого, тобто
- матриця переходу від першої бази до другого, тобто  . Тоді
. Тоді 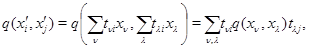 звідки видно, що зміна матриці простору
звідки видно, що зміна матриці простору 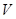 при зміні бази описується співвідношенням
при зміні бази описується співвідношенням 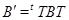 .
.
Якщо 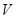 - абстрактний векторний простір з базою
- абстрактний векторний простір з базою  й
й 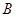 - довільна знакозмінна
- довільна знакозмінна 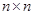 - матриця над
- матриця над 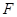 , то існує єдиний спосіб перетворити
, то існує єдиний спосіб перетворити  в знакозмінний простір, таке, що
в знакозмінний простір, таке, що 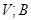 в
в  , а саме, покласти
, а саме, покласти 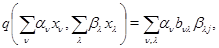 , де
, де  - елемент, що стоїть в матриці
- елемент, що стоїть в матриці 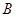 на місці
на місці 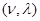 . Пропозицію 8 Припустимо, що
. Пропозицію 8 Припустимо, що 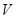 - знакозмінний простір,
- знакозмінний простір, 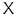 - його база й
- його база й 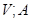 в.
в. 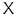 Тоді матричний ізоморфізм, певний базою
Тоді матричний ізоморфізм, певний базою 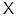 , відображає
, відображає  на групу всіх оборотних
на групу всіх оборотних 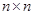 - матриць
- матриць  над
над 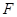 , що задовольняють співвідношенню
, що задовольняють співвідношенню 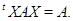
Дискримінантом 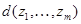 векторів
векторів 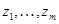 у знакозмінному просторі
у знакозмінному просторі  називається визначник
називається визначник 
Зокрема, якщо  - база простору
- база простору 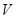 й
й 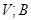 у цій базі, те
у цій базі, те 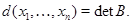 Якщо
Якщо 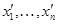 - інша база, то співвідношення
- інша база, то співвідношення 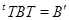 показує, що
показує, що 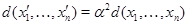 для якогось
для якогось 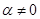 із
із 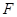 . Отже, канонічний образ елемента
. Отже, канонічний образ елемента  в
в  не залежить від бази; він називається дискримінантом знакозмінного простору
не залежить від бази; він називається дискримінантом знакозмінного простору 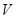 й позначається через
й позначається через 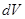 . Тут множина
. Тут множина  визначається очевидним образом: беремо
визначається очевидним образом: беремо 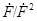 , приєднуємо до неї нуль 0 і думаємо, що добуток нуля й будь-якого іншого елемента дорівнює нулю. Запис
, приєднуємо до неї нуль 0 і думаємо, що добуток нуля й будь-якого іншого елемента дорівнює нулю. Запис 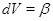 , де
, де 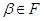 , буде позначати, що
, буде позначати, що 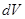 дорівнює канонічному образу елемента
дорівнює канонічному образу елемента  в
в  або, інакше кажучи, що
або, інакше кажучи, що 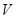 має базу
має базу  , для якої
, для якої  . Якщо
. Якщо 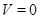 , то думаємо
, то думаємо 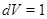 .
.
Приклад 9Розглянемо знакозмінний простір 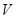 зі знакозмінною формою
зі знакозмінною формою 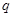 . Нехай
. Нехай  - його база, а
- його база, а 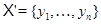 - сполучена база сполученого простору
- сполучена база сполученого простору 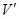 . Нехай
. Нехай  в.
в. 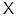 Тоді
Тоді 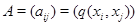 . Легко бачити, що матриця лінійного перетворення
. Легко бачити, що матриця лінійного перетворення 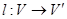 , певного раніше, щодо баз
, певного раніше, щодо баз 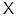 і
і 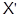 дорівнює
дорівнює  ; дійсно, якщо
; дійсно, якщо 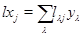 , те
, те
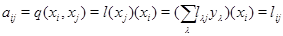
Аналогічно матриця перетворення 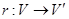 щодо баз
щодо баз 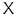 і
і  дорівнює
дорівнює 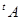 .
.
Пропозиція 10 Будь-які 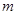 векторів
векторів 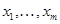 знакозмінного простору
знакозмінного простору  , такі, що
, такі, що  , лінійно незалежно.
, лінійно незалежно.
Доказ. Залежність  спричиняє
спричиняє 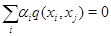 для
для 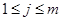 . Це означає залежність між рядками матриці
. Це означає залежність між рядками матриці 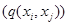 , що неможливо, тому що дискримінант не дорівнює 0.
, що неможливо, тому що дискримінант не дорівнює 0.
Пропозиція11 Наступні твердження для знакозмінного простору  рівносильні:
рівносильні:
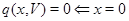 ,
,
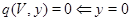 ,
,
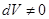 ,
,
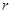 біективно,
біективно,  біективно.
біективно.
Доказ. Можна вважати, що  . Зафіксуємо базу
. Зафіксуємо базу 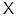 простору
простору  , і нехай
, і нехай  - сполучена база. Нехай
- сполучена база. Нехай  в.
в. 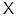 Через
Через
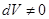
| 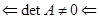
|
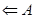 оборотна оборотна 
| |
 біективно, біективно,
|
тому (3) рівносильне (5). Аналогічно (3) рівносильне (4). Далі
 біективно біективно
| 
|
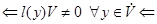
| |
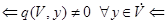
| |
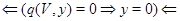
| |
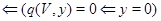 , ,
|
так що (5) рівносильне (2). Нарешті, мабуть, що (2) рівносильне (1).
Визначення 12Знакозмінний простір 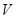 називається регулярним, якщо воно задовольняє одному з п'яти рівносильних умов. Знакозмінний простір
називається регулярним, якщо воно задовольняє одному з п'яти рівносильних умов. Знакозмінний простір 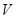 називається виродженим, якщо воно не є регулярним. Нарешті, воно називається цілком виродженим, якщо
називається виродженим, якщо воно не є регулярним. Нарешті, воно називається цілком виродженим, якщо 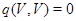 .
.
Якщо 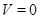 , то
, то 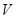 регулярно. Якщо
регулярно. Якщо  , то через і
, то через і
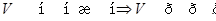
Пропозиція.13 Нехай 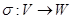 - уявлення знакозмінних просторів. Якщо
- уявлення знакозмінних просторів. Якщо  регулярно, то
регулярно, то 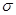 - ізометрія.
- ізометрія.
Доказ. Візьмемо 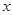 з ядра уявлення
з ядра уявлення 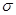 . Тоді
. Тоді 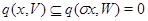 . Звідси через регулярність простору
. Звідси через регулярність простору 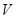 одержуємо, що
одержуємо, що 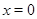 .
.
Пропозиція 14Кожній базі 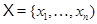 регулярного знакозмінного простору
регулярного знакозмінного простору  відповідає єдина база
відповідає єдина база  цього простору, називана сполученої до
цього простору, називана сполученої до 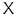 відносно
відносно 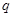 й така, що
й така, що  для всіх
для всіх 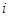 ,
, 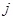 . Якщо
. Якщо  в
в 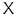 и
и 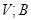 в
в 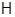 , то
, то  .
.
Доказ.1) Покладемо  для
для 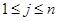 , де
, де 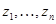 - сполучена до
- сполучена до 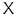 база сполученого простору
база сполученого простору 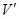 . Тоді
. Тоді 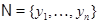 - база, тому що
- база, тому що  біективно. Крім того,
біективно. Крім того, 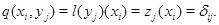 . Цим доведене існування бази
. Цим доведене існування бази 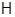 . Одиничність безпосередньо треба з регулярності. 2) Нехай
. Одиничність безпосередньо треба з регулярності. 2) Нехай 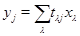 . Тоді
. Тоді 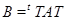 й
й  Звідси
Звідси 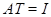 , так що
, так що 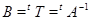 й
й  .
.
Розглянемо знакозмінний простір 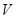 зі знакозмінною формою
зі знакозмінною формою  . Будемо говорити, що
. Будемо говорити, що 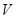 має ортогональне розкладання
має ортогональне розкладання  на підпростори
на підпростори 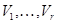 якщо воно є прямою сумою
якщо воно є прямою сумою 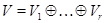 з попарно ортогональними
з попарно ортогональними  , тобто
, тобто 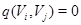 при
при 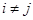 . Назвемо
. Назвемо 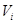 компонентами цього ортогонального розкладання. Будемо говорити, що підпростір
компонентами цього ортогонального розкладання. Будемо говорити, що підпростір 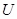 розщеплює
розщеплює 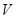 або що
або що 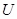 є компонентом простору
є компонентом простору 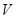 , якщо існує підпростір
, якщо існує підпростір 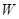 простору
простору 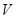 , таке, що
, таке, що 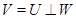 . Маємо
. Маємо  де добуток береться в.
де добуток береться в. 
Розглянемо два знакозмінних простори 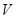 й
й 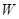 над тим самим полемо
над тим самим полемо  й припустимо, що є ортогональне розкладання
й припустимо, що є ортогональне розкладання  , а
, а 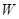 - сума просторів
- сума просторів 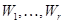 ,
, 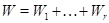 , причому
, причому  при
при 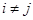 . Нехай для кожного
. Нехай для кожного 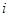 ,
, 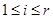 , задане уявлення
, задане уявлення  . Тоді, як відомо з лінійної алгебри, існує єдине лінійне перетворення
. Тоді, як відомо з лінійної алгебри, існує єдине лінійне перетворення 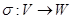 , що погодиться з кожним
, що погодиться з кожним 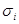 на
на 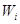 . Насправді легко перевірити, що
. Насправді легко перевірити, що 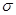 - уявлення. Ми будемо записувати його у вигляді
- уявлення. Ми будемо записувати його у вигляді 
Важливим є випадок, коли  ,
,  для всіх
для всіх 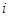 і
і 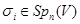 для всіх
для всіх 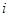 ; тоді
; тоді 
Якщо дано ще одне таке уявлення  , то
, то

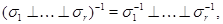
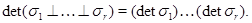
Розглянемо знакозмінний простір 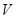 над полем
над полем  . Під ортогональним доповненням підпростору
. Під ортогональним доповненням підпростору 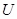 простору
простору 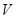 в
в 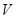 розуміється підпростір
розуміється підпростір
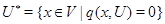
співпадаюче також з
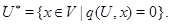
Визначимо радикал простору 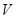 як підпростір
як підпростір 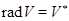 . Очевидно,
. Очевидно,
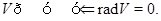
Пропозиція15 Нехай 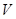 - знакозмінний простір, що є сумою попарно ортогональних підпросторів, тобто
- знакозмінний простір, що є сумою попарно ортогональних підпросторів, тобто 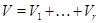 , де
, де 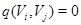 при
при 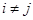 . Тоді
. Тоді
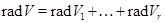 ,
,
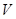 регулярно
регулярно 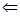 кожне
кожне  регулярно,
регулярно,
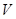 регулярно
регулярно 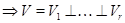 .
.
Доказ. (1) Візьмемо в  довільний елемент
довільний елемент  і запишемо його у вигляді
і запишемо його у вигляді  ,
, 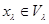 . Тоді
. Тоді
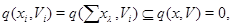
так що 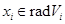 , звідки
, звідки 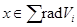 . Обернено, якщо
. Обернено, якщо 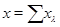 , де
, де 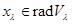 , те
, те  звідки
звідки 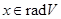 . (2) Це треба з (1) і того, що знакозмінний простір регулярний тоді й тільки тоді, коли його радикал дорівнює
. (2) Це треба з (1) і того, що знакозмінний простір регулярний тоді й тільки тоді, коли його радикал дорівнює 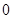 . (3) Якщо
. (3) Якщо  ,
, 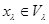 , те
, те
 2020-04-20
2020-04-20 206
206