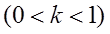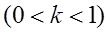Еліптичні інтеграли 1-го, 2-го і 3-го роду

 

Тепер залишається вивчити найпростіші з інтегралів виду (8), до яких можна було б звести всі інтеграли цього виду, а відповідно, в кінцевому рахунку, і взагалі, всі еліптичні інтеграли.

Виділимо з раціональної функції R(x), що зустрічається в підінтегральному виразі (8) цілу частину P(x), а правильний дріб, який входить до його складу, розкладемо на прості дроби. Якщо не об’єднувати спряжені комплексні корені знаменника, а розглядати їх окремо, як дійсні корені, то R(x) представиться у вигляді суми степенів 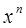(n = 0, 1, 2,…) і дробів виду  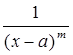(m = 1, 2, 3,…), де а може бути і уявним числом, помножених на числові коефіцієнти. Звідси ясно, що інтеграл (8), в загальному випадку, являється лінійним агрегатом наступних інтегралів:

 

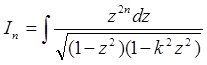 (n = 0, 1, 2,…)

 

і 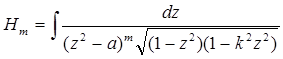(m = 1, 2, 3,…).

Зупинимося на інтегралах 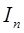. Якщо проінтегрувати тотожність

 

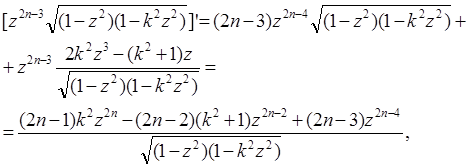
то отримаємо рекурентне співвідношення

 

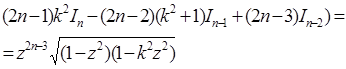 (9)

 

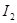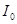що зв’язують три послідовні інтеграли І. Припускаючи що тут n=2, виразимо  через  та 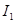; якщо взяти n=3 і замість  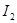підставити його вираз через  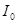та 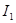, то навіть  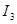виразиться через ці інтеграли. Продовжуючи так далі, легко переконатися, що кожен з інтегралів  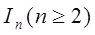виражається через  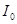та 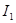 і далі враховуючи (9), можна встановити і вигляд з’єднуючої їх формули

 

 

 

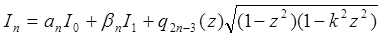
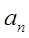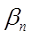де  і  - постійні, а  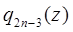є непарний многочлен степені (2n-3). Звідси стає зрозумілим, що якщо  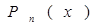є многочлен n – ї степені від х, то

 

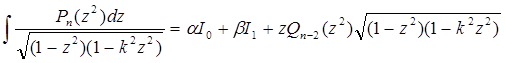, (10)

 

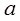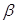де  і  - постійні, а 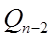(х) є деякий многочлен (n-2) – ї степені від х. Визначення цих постійних і коефіцієнтів многочлена Q може бути виконано (якщо многочлен Р коректно заданий за методом невизначених коефіцієнтів.)

Зауважимо, що з (9) можна було б виразити через 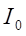 та 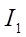інтеграли  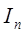і при від’ємних значеннях (n = -1, -2, …), так що в інтегралах  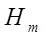досить обмежитись випадком .

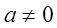Переходячи до інтегралів 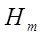 (скажімо, при дійсних a), подібним чином встановимо для них рекурентне співвідношення

 

 

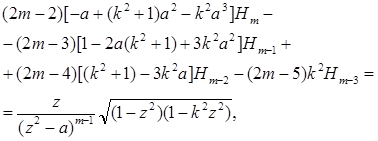
справедливе і при від’ємних і нульовому значеннях m.

Звідси всі 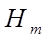 виражаються через три з них:

 

 

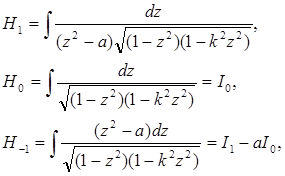
тобто, кінцево через 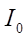,  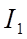та .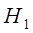

Підкреслимо, що усе це зберігає силу і при уявних значеннях параметра а.

Так в результаті усіх наших тверджень ми підходимо до наступних висновків: всі еліптичні інтеграли за допомогою елементарних підстановок – з точністю до доданків, що виражаються в кінцевому виді, - приводяться до наступних трьох стандартних інтегралів:

 

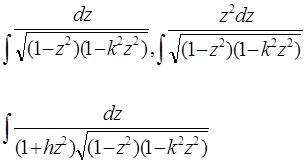
(останній інтеграл виходить із 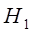 введенням, замість 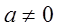, нового параметра 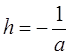). Ці інтеграли, як показав Ліувіль, в кінцевому виді вже не беруться. Лежандр їх назвав еліптичними інтегралами, відповідно, 1-го, 2-го і 3-го роду. Перші два містять лише один параметр k, а останній, крім нього, ще (комплексний) параметр h.

Лежандр вніс у ці інтеграли ще подальші спрощення, виконавши в них підстановку 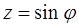 ( 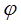змінюється від 0 до 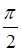). При цьому перший із них безпосередньо переходить в інтеграл

 

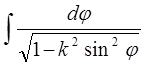. (11)

 

Другий перетворюється так:

 

 

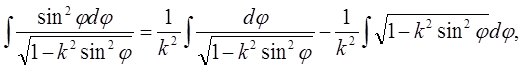
тобто приводиться до попереднього інтеграла і до нового інтеграла

 

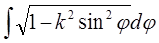. (12)

 

Нарешті, третій інтеграл при вказаній підстановці переходить в

 

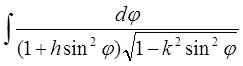. (13)

 

Інтеграли (11), (12) і (13) також називаються еліптичними інтегралами 1-го, 2-го і 3-го роду – в формі Лежандра.

Із них особливо важливе значення і застосування мають перші два. Якщо враховувати, що ці інтеграли при 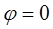перетворюються в нуль, і тим зафіксувати вільні сталі, що містяться в них, то отримаємо дві доволі визначені функції від 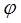, які Лежандр позначив відповідно через F(k, φ) і E(k, φ). Тут, крім незалежної змінної 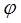, вказаний також параметр k, що називається модулем, який входить у вирази цих функцій.

Лежандром були складені обширні таблиці значень цих функцій при різних 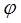 і різних k. В них не тільки аргумент 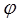,який трактуються як кут, що виражається в градусах, але і модуль k розглядається як синус деякого кута 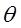, який і вказується в таблиці замість модуля, причому також в градусах.

Крім того, як Лежандром, так і іншими вченими були вивчені найглибші властивості цих функцій, встановлений ряд формул, що відносяться до них, і т.д.

Дякуючи цьому функції F і E Лежандра ввійшли в сім’ю функцій, що зустрічаються в аналізі і його додатках, на рівних правах з елементарними функціями.

 

Висновки

 

В результаті усіх наших міркувань ми коротко можемо сказати, що всі еліптичні інтеграли за допомогою елементарних підстановок – з точністю до доданків, що виражаються в кінцевому виді, - приводяться до наступних трьох стандартних інтегралів Лежандра:

 

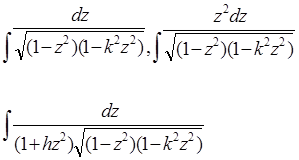
А за допомогою підстановки 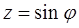 ( 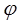змінюється від 0 до 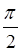) ці інтеграли перетворюються в так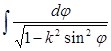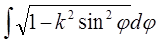і:

 

 ,  і ,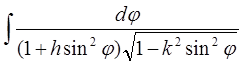

 

які також називаються еліптичними інтегралами 1-го, 2-го і 3-го роду в формі Лежандра, значення яких можна знайти в таблицях.

 

Використана література:

 

1. Г.М. Фихтенгольц. Курс дифференциального и интегрального исчисления. Том I. М.: Наука, 1966 г., 800 стр. с илл.

2. Г.М. Фихтенгольц. Курс дифференциального и интегрального исчисления. Том II. М.: Наука, 1966 г., 800 стр. с илл.

3. Г. Корн, Т. Корн. Справочник по математике для научных работников и инженеров. М.: Наука, 1973 г., 832 стр. с илл.

4. И.Н. Бронштейн, К.А. Семендяев. Справочник по математике для инженеров и учащихся вузов. М.: Наука, 1980 г., 976 с., илл.

ДОДАТКИ