Тема 7. АЛГОРИТМЫ УПРАВЛЕНИЯ ПНК.
Общая характеристика алгоритмов в этой группе приведена в разделе 3.1.3. Из изложенного в упомянутом разделе следует, что АУПНК делятся на целевые, решающие определенную функциональную задачу (управление ПНК, управление траекторным движением, посадкой, выход на ЛЗП и т.п.), и специфические, организующие заданное качество процессов управления, движения и т.д. (оптимизация режимов полета, терминального управления, точностных характеристик). Из всего многообразия алгоритмов управления остановимся на алгоритмах управления полетом по маршруту (горизонтальный, вертикальный профиль).
Алгоритмы управления реализуются в вычислителе ВСС, командные сигналы с которой обрабатываются ВСУП, ВСУУ, ВСУТ для непосредственного управления ЛА (п.1.3). ВСС вырабатывает сигнал исходя из навигационных определений. ВСУП, ВСУТ переводит эти сигналы через определенные законы управления в командные сигналы пилотирования (связь НК и ПК).
Анализ управления и движений ЛА.
7.1.1. Выбор закона управления [13].
Одна из основных задач полета – выдерживание ЛЗП и организация переходов с одной ЛЗП на другую.
Реализация этих задач связана с обеспечением бокового движения ЛА с необходимыми параметрами, для чего необходимо:
-формирование в ВСС сигналов и команд управления, которые в современных ПНК сводятся к формированию  и признаков готовности боковой программы
и признаков готовности боковой программы
- организовать связь ВСС (НК) и ВСУП (ПК) по каналу заданного крена  ;
;
- обеспечить в ВСУП (ПК) автоматическое выдерживание 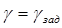 .
.
От вида и содержания управляющего сигнала в значительной степени зависит боковое уклонение самолета от ЛЗП особенно при переходных процессах (выход на ЛЗП, смена ЛЗП).
При рассмотрении бокового движения будем базироваться на упрощенных уравнениях движения, предполагающих:
- контур стабилизации движения вокруг ц.м. и канал бокового управления независимы (это допустимо, т.к. собственные частоты контуров существенно различны и боковой длинно периодический канал не влияет на стабилизацию угловых движений);
- полет горизонтальный;
- скольжение отсутствует.
Для указанных условий при наличии крена и без скольжения уравнения имеют вид:
 (7.1)
(7.1)
где V- скорость самолета, P- сила тяги, Q – лобовое сопротивление, P(a-j) – вертикальная составляющая силы тяги, Y – подъемная сила; 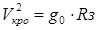 ; Rз – радиус Земли; g, y - крен и курс;
; Rз – радиус Земли; g, y - крен и курс;  - ускорение свободного падения на высоте и на уровне моря.
- ускорение свободного падения на высоте и на уровне моря.
Т.к. для самолета V<<Vкро, то в (7.1) во втором уравнении можно пренебречь центростремительным ускорением, обусловленным кривизной земной поверхности и поделив после пренебрежения третье уравнение на второе (7.1) получаем:
 (7.2)
(7.2)
Для магистральных самолетов обычно g< 25°-30°, особенно в автоматических режимах, поэтому:
 (7.3)
(7.3)
Будем рассматривать движение в прямоугольной СК Z, d. Будем считать, что за время переходного процесса (£ 3 мин) при смене ЛЗП Vв=const и U=const.

Формулы (7.2), (7.3) можно получить проще:
 (1)
(1)

 Если условие (1) нарушается – вираж со скольжением.
Если условие (1) нарушается – вираж со скольжением.
Для горизонтального движения:
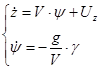 (7.4)
(7.4)
(разворот координирован; tg g»g; sin y»y; U=const; V=const; g=gзад, 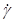 неограниченна, моментами инерции ЛА можно пренебречь).
неограниченна, моментами инерции ЛА можно пренебречь).
Систему (7.4) можно представить в виде (продифференцировав и исключив 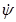 ):
):
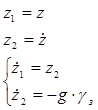 (7.5)
(7.5)
Определим 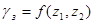 , оценивая качество системы функционалом:
, оценивая качество системы функционалом:
 (7.6)
(7.6)
Физический смысл этого функционала: первый член – учитывает площадь под интегральной кривой z(t), обеспечивая min отклонение от ЛЗП; второй член – обеспечивает предотвращение больших скоростей в начале процесса и т.о. обеспечивая перерегулирование и устойчивость; третий член ограничивает мощность управляющего сигнала. Весовые коэффициенты  устанавливают потребность различной точности для разных координат (чем выше точность, тем больше коэффициенты).
устанавливают потребность различной точности для разных координат (чем выше точность, тем больше коэффициенты).
Т.о. задача сводится к нахождению только 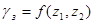 под действием которого система (7.4) переходит из состояния
под действием которого система (7.4) переходит из состояния  в состояние
в состояние  и при этом функционал J принимал бы min значение.
и при этом функционал J принимал бы min значение.
Решение такой задачи ведется методом динамического программирования. Уравнение динамического программирования Белмана:
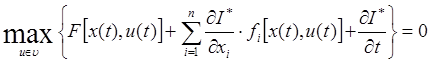 (7.7)
(7.7)
где управление 

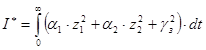

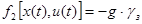
После подстановки имеет вид:
 (7.8)
(7.8)
для нахождения значения  , дост. min функционала J, приравняем 0 производную по
, дост. min функционала J, приравняем 0 производную по  от левой части
от левой части
 (7.9)
(7.9)
Исключив из (7.8) и (7.9)  получаем:
получаем:
 (7.10)
(7.10)
Решение этого нелинейного уравнения ищем в виде квадратичной формы:
 (7.11)
(7.11)
После подстановки (7.11) в (7.9):
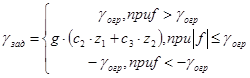 (*)
(*)
Подставляя I* в (7.10) и приравнивая коэффициенты при 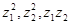 к нулю, получаем соотношения между коэффициентами функции I*:
к нулю, получаем соотношения между коэффициентами функции I*:
 (7.12)
(7.12)
Решение (7.11) приводит к функции I*, являющейся функцией Ляпунова, гарантирующей асимптотическую устойчивость замкнутой системы.
Характеристический многочлен замкнутой системы принимает вид:
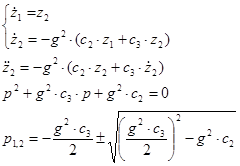
При известных  из (7.12) определяются
из (7.12) определяются  и
и  . Однако
. Однако  не неизвестны. Необходимо задаться дополнительными требованиями к характеру переходного процесса исходя из специфики полета. Например: отсутствие перерегулирования при
не неизвестны. Необходимо задаться дополнительными требованиями к характеру переходного процесса исходя из специфики полета. Например: отсутствие перерегулирования при  . Оно обеспечивается при вещественных
. Оно обеспечивается при вещественных  , и min
, и min  при
при  .
.
При этом:
 (7.13)
(7.13)
Т.о. решение уравнения Беллмана показано, что оптимальное в смысле I* качество переходного процесса может быть обеспечено линейным законом управления.
 (7.13*)
(7.13*)
где  при кратных корнях характеристического уравнения.
при кратных корнях характеристического уравнения.
Обозначив  получим решение (7.13) в виде:
получим решение (7.13) в виде:
 (7.14)
(7.14)
t- величина обратная корню характеристического уравнения (а корни кратные).
Для обеспечения правильного разворота в направлении к ЛЗП при любых z, в закон управления необходимо ввести ограничение по z:

Выбирается 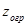 из следующих соображений.
из следующих соображений.
При любых  самолет должен следовать к ЛЗП. Это будет обеспечено, если:
самолет должен следовать к ЛЗП. Это будет обеспечено, если:
 при g=0.
при g=0.
где  где
где  - угол подхода к ЛЗП.
- угол подхода к ЛЗП.
Отсюда следует:
 (7.15)
(7.15)
Если принять за t=0 время достижения самолетом значений боковой координаты  при g=0, то дальнейшее его движение будет описываться уравнениями:
при g=0, то дальнейшее его движение будет описываться уравнениями:
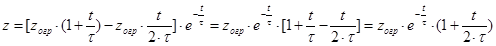

 2020-04-20
2020-04-20 155
155







