Вплив середньої за величиною головної напруги. Спрощений вигляд рівняння пластичності

Невеликі розбіжності при розрахунках за рівнянням (93) і (91), яке не враховує вплив величини σ₂ на перехід в пластичний стан, показують, що вплив σ₂ не дуже істотний. Визначимо цей вплив на результати розрахунків за рівнянням (93). Введемо безрозмірну величину (параметр Надаї - Лод)

    ξ_σ = [σ₂ – (σ₁ + σ₃)/2]/(σ₁ - σ₃)/2 = (2σ₂ – σ₁ – σ₃)/(σ₁ – σ₃),         (107)

    звідкіля

               σ₂ = ξσ(σ₁ - σ₃)/2 + (σ₁ + σ₃)/2.                                     (108)

    Підставляючи (108) в рівняння (107), отримуємо

      [σ₁ - ξ_σ(σ₁ - σ₃)/2 - (σ₁ + σ₃)/2]² + [ξ_σ(σ₁ - σ₃)/2 + (σ₁ + σ₃)/2 – σ₃] +

                                    + (σ₁ - σ₃)² = 2σ_т².

Далі

    (σ₁ - σ₃)²[(1 - ξ_σ)/2]² + (σ₁ - σ₃)²[(1 + ξ_σ)/2]² + (σ₁ - σ₃)² = 2σ_т².

                       (σ₁ - σ₃)² = [(4/(3 + ξ_σ²)]σ_т².

                         σ₁ - σ₃  = (2/ )σ_т.

Позначимо 2/ 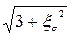 = β, тоді

                               σ₁ - σ₃ = βσ_т.                                                                                            (109)

     Тут β – коефіцієнт, що враховує вплив напруги σ₂ на умову пластичності. Рівняння (109) являє собою спрощений вид рівняння пластичності в головних осях, в якому вплив напруги σ₂ відображено коефіцієнтом β. Враховуючи, що σ₁ ≥ σ₂ ≥ σ₃, визначимо вид рівняння пластичності для крайніх випадків, коли σ₂ одно одному з двох інших головних напружень. Візьмемо випадок σ₂ = σ₁. Тоді

ξ_σ = (2σ₁ – σ₁ – σ₃)/(σ₁ – σ₃) = 1, β = 2/  = 1.

В іншому крайньому випадку σ₂ = σ₃. Тут ξ_σ = (2σ₃ – σ₁ – σ₃)/(σ₁–σ₃) = - 1,

    β = 2/  = 1. Отримали, що якщо дві головних напруги рівні між собою, то β = 1. Візьмемо проміжне значення σ₂=(σ₁+σ₃)/2. Воно виконується для плоского деформованого стану. Маємо

      ξ_σ = [2(σ₁ + σ₃)/2 – σ₁ – σ₃)]/(σ₁ – σ₃) = 0, β = 2/  ≈ 1.155.

      Коефіцієнт β названий коефіцієнтом Лодьє, на ім'я вченого, експериментально досліджував його значення. Добуток βσ_т іноді називають вимушеною межею плинності і позначають σ_т*.

Рис.27. Залежність

коефіцієнта Лодьє

від напруги σ₂

 

    Зміни значень коефіцієнта Лодьє в усьому можливому інтервалі зміни значень σ₂ показані на рис. 27. Як видно, при рівності двох головних напруг - або σ₂ =σ₃, або σ₂=σ₁ - рівняння пластичності має вигляд σ₁-σ₃=σ_т, тобто збігається з рівнянням (91). У всіх інших випадках чисельні розбіжності між цими умовами різні, найбільшу розбіжність порядку 15% має місце при σ₂=σ_ср, тобто при плоскому деформованому стані. У цьому випадку рівняння пластичності в головних осях має вигляд σ₁-σ₃=1,15σ_т (точніше 1,155σ_т).

Рівняння (109), як і рівняння (91) і (93), показує, що перехід в пластичний стан залежить не від абсолютної величини головних напруг, а від їх різниці. Збільшення або зменшення головних напружень на одну і ту ж величину змінить кульової тензор напружень та пружну деформацію об’єму, але не позначиться на виконанні рівняння пластичності.

Рівняння пластичності повинна виконуватися при будь-якому рішенні пластичних задач і обов'язково включається в систему рівнянь, що використовуються для вирішення.

 

Лекція 9

Асоційований закон пластичного плину. Співвідношення Леві-Мізеса. ГДЕ ОНИ?Постановка задач в теории пластичності. Повна система рівнянь та граничних умов теорії пластичності

 

    Вирішити задачи в теорії пластичності або теорії пружності значить за даними умовами на поверхні (задані поверхневі сили або напруги і (або) зсуву) визначити тензори напруг і деформацій і зміщення за об’ємом тіла, тобто виразити всі компоненти напружень, деформацій і зсувів у вигляді функцій координат σ_х = φ₁(x, y, z), … τ_xy = φ₄(x, y, z), … ε_x = φ₇(x, y, z) … і т.д.

    Така задача називається прямою, для визначення всіх 15 невідомих потрібна система з 15 рівнянь. Цю систему складають 3 статичних рівняння рівноваги, 6 геометричних рівнянь зв'язку деформацій і зсувів та 6 фізичних рівнянь зв'язку напруг і деформацій (узагальнений закон Гука). Іноді вирішується зворотна задача - по заданому полю компонент напружень, деформацій і зсувів необхідно визначити зовнішні навантаження, що забезпечують такі поля. Найбільш часто звертаються до змішаних задач, в яких частина зовнішніх навантажень і компонент напруг, деформацій і зсувів задана, а інші визначаються з рішення.

Задачи, пов'язані з умовами на кордоні інструменту - деформується метал і дозволяють розраховувати будь-які параметри напружено-деформованого стану за об’ємною зони деформації або тільки на контактній поверхні (задача з визначення полів напружень, деформацій і зсувів або деяких з цих компонент), особливо інженерні, в теорії ОМТ зазвичай називають крайовими.

Крайові задачі відносяться до розв'язання диференціальних рівнянь. Диференціальні рівняння дозволяють виразити співвідношення між змінами (приростами) фізичних величин і широко використовуються в теорії пластичності і як її програми - у теорії обробки металів тиском.

Звичайним диференціальним рівнянням називають рівняння, що включає незалежну змінну х, шукану функцію y = φ (x), а також її похідні різних порядків. Рішення диференціального рівняння зводиться до відшукання функцій, які задовольняють вихідне диференціальне рівняння на всій довжині заданого проміжку зміни координати х, за якої змінюється шукана фізична величина. Підстановка отриманого шуканого рівняння та його часткових похідних у вихідне диференціальне рівняння має звертати останнє в тотожність.

Рішення крайової задачі має задовольняти деяким умовам на кінцях заданого кінцевого або нескінченного проміжку при х = a та x = b зміни незалежної змінної на початку деформації (початковим умовам) і значенням в точках а і b в будь-який момент часу (крайовим умовам). При строгій постановці необхідно задавати початкові та крайові умови в вигляді односторонніх похідних, що характеризують напрямок зміни параметра на краях проміжку. У теорії ОМТ найчастіше задають певні значення шуканого параметра в точках a і b. Інтегрування (рішення) диференціального рівняння дозволяє знайти потрібну функцію і довільні постійні (постійні інтегрування).

Крайова задача поставлена коректно, якщо вона відповідає таким вимогам:

- Рішення повинно існувати, на нього не повинно накладатися суперечать один одному обмеження;

- Рішення має бути єдиним, неоднозначність і невизначеність рішення повинні бути виключені;

- Рішення має бути стійким, безперервно залежати від вихідних даних. Невеликі зміни змінними параметрами повинні призводити до невеликих змін шуканої функції. Деякі спрощення і відхилення від реальних процесів допустимі, якщо вони не викликають великих похибок у рішенні.

Постановка задач в теорії ОМТ не завжди відповідають цим вимогам. Використовувані системи рівнянь можуть включати диференціальні рівняння в часткових похідних одночасно з лінійними алгебраїчними рівняннями. Рішення замкнутої системи рівнянь називають моделюванням, а саму систему - моделлю процесу ОМД.

Математичні моделі, які використовуються в теорії ОМТ, не обов'язково включають диференціальні рівняння. Так, метод верхньої оцінки не використовує диференціальних рівнянь, метод ліній ковзання не забезпечує однозначність рішення. Обидва названих методу грунтуються на розривних рішеннях. При цьому будь-які замкнуті системи рівнянь, що дозволяють визначити напруги, деформації і зміщення або хоча б деякі з цих параметрів, що виникає під дією напруги з боку деформуючого інструменту, називають крайовими задачами. Крайова задача для пластичнї течії повинна включати (у явному чи не в явному вигляді) рівняння пластичності.

Складність постановки крайових задач пов'язана і з формулюванням граничних умов. Для нестаціонарних процесів граничні умови систематично змінюються по ходу процесу (у часі). Для стаціонарних процесів початкова та кінцева стадії також є нестаціонарними. Протяжність контакту металу з інструментом і положення меж зони деформації в багатьох випадках невідомі.

Безперечним є положення про відсутність напруги, нормальних щодо поверхні, вільної від впливу інструменту, відсутність зсувів на контакті на лінії (в точці) розділу течії. Перехід до тисків на краях контакту з допомогою рівняння пластичності не викликає сумнівів, якщо вони є головними напруженнями. Не для всіх процесів тиску є головними напруженнями.

Постановка завдань іноді включає суперечність фізичним закономірностям граничні умови. Так, припущення про повну прилипанні на контакті супроводжується допущенням про відсутність напруги тертя або про досягнення граничних значень напружень тертя. У зоні прилипання діють напруги тертя спокою, величина яких визначається умовами мінімуму роботи деформації. Граничні умови не можна формулювати для всієї поверхні контакту без урахування того, що контактні напруги і вздовж металу самовстановлюється відповідно до закону мінімальної роботи, і з умовами деформації. Ряд припущень про граничні умови на контактній поверхні в дійсності є частковим апріорним вирішенням задачи.

У нестаціонарних процесах зростання деформації змінює не тільки абсолютні розміри пластичної зони, але і співвідношення між ними, що викликає зміну граничних умов на контакті. Якщо на початку деформації високих смуг вирішальний вплив на напружено-деформований стан роблять зовнішні зони, то при зменшенні товщини їх вплив зменшується, і все більший вплив починають надавати напруги тертя, тобто граничні умови систематично змінюються. У стаціонарних процесах граничні умови залежать від геометрії зони деформації. Для одного і того ж виду процесу (прокатки, волочіння, пресування) зміна геометрії може викликати зміну граничних умов. Тому вирішення завдань обмежують для процесів, подібних з геометрії. Як показники подібності в процесах з обтисненням використовують відношення довжини контакту до середньої висоті зони деформації (фактор форми), для процесів вигину - відношення товщини деформованого металу до діаметру вигину або відношення діаметра полого вироби (труби) до товщини стінки.

Ці та інші положення показують, що рішення, які використовуються в теорії ОМТ, не повною мірою відповідають поняттям крайових задач. У цілому термін «крайові задачі» стосовно до теорії ОМТ можна розглядати як моделювання умов взаємодії інструмента і деформованого металу з певними, іноді грубими допущеннями. Отримані рішення повинні проходити апробацію стосовно практичних умов ОМД. Деякі наведені вище положення більш докладно розглядаються далі.

У теорії пружності задачу вирішують у пружній постановці, коли постулюють суворе виконання узагальненого закону Гука. У теорії пластичності розглядають пружно-пластичну задачу, коли враховують і пружні і невеликі пластичні деформації, і задачу з великими пластичними деформаціями. В останньому випадку пружними деформаціями нехтують зважаючи на їх малості в порівнянні з пластичними. Для вирішення необхідно залучати довідкові величини, в пружних задачах це модулі пружності і коефіцієнт Пуассона, у пластичних - показники міцнісних властивостей металу. Поняття меж пропорційності і пружності в рішеннях і пружних і пластичних завдань не використовуються. Важливим є тільки значення межі або напруги плинності, що визначає перехід від пружної деформації до пластичної.

Необхідність використання понять межі текучості σ_0,2(або σ_s) і напруги плинності σ_т пов'язана з тим, що перехід до пластичної течії викликає одночасне зміцнення металу та підвищення величини напруг, необхідних для продовження пластичної деформації (інтенсивності напружень ε_і). Приріст роботи, необхідної для продовження пластичної деформації, на можливих зсувах завжди максимально. Це положення, відоме як постулат Друккер, засноване на припущенні про підвищення механічних властивостей у результаті деформації по будь-якому напрямку. Підвищення міцності тіла і відповідна зміна умови переходу до пластичного стану позначається на розрахунку зсувів (асоційований закон течії).

Якщо приріст роботи деформації максимальний, то повна робота деформації завжди мінімальна.

Рішення задач при одночасному визначенні розподілу напружень, зсувів і деформацій, можливо по двох напрямках.

У теорії плину визначають збільшення прирісту компонент деформацій з використанням узагальненого закону Гука, але замість тензора кінцевих деформацій розглядають тензор нескінченно малих приростів компонент деформацій, викликаних нескінченно малими приростами напруг. Для пружно-пластичних деформацій отримують

    dε_x = (1/E)[dσ_x – μ(dσ_y – dσ_z)] + (3/2)(dε_и /σ_и)(σ_x – σ_cp)  

                 dγ_zx = dτ_zx/G + 3dε_и /σ_и)(τ_zx),                       

    де  dε_x, dγ_zx и dσ_x, dτ_zx – відповідно збільшення деформацій і напруг, σ_cp - середня нормальна напруга, Е, G - модулі пружності першого та другого роду, μ - коефіцієнт Пуассона, ε_і, σ_і - відповідно інтенсивності деформацій і напруг. Перший доданок кожного з шести рівнянь визначає приріст пружної деформації, друге - пластичної. Якщо пружними деформаціями нехтують, рівняння приводяться до виду

                  dε_x = (3/2)(dε_и/σ_и)(σ_x – σ_cp) і т.д.

                       dγ_zx = dτ_zx/G + 3dε_и/σ_и)(τ_zx).                       

    Розділивши обидві частини кожного з 6 рівнянь на dt (взявши похідну за часом) і враховуючи, що dε_і/dt є інтенсивність швидкостей деформації ξ_і, отримуємо залежність компонентів швидкостей деформації від компонентів девіатора напруг (рівняння Сен-Венана - Леві - Мізеса)

                             ξ_x = (3/2)(ξ_и/σ_т)(σ_х – σ_ср)   і т.д.

Використання понять швидкостей деформацій, як і понять швидкостей переміщень, не означає обліку фактора часу при визначенні пластичних деформацій. Це можливість переходу від прирісту компонент деформацій і напруг до абсолютних значень компонент швидкості деформації та напружень при подальшому інтегруванні по часу.

Теорія малих пружно-пластичних деформацій грунтується на понятті простого навантаження. Під простим навантаженням розуміється такий додаток навантаження, при якому всі компоненти тензора напружень і відповідно компоненти девіатора напруг зростають пропорційно одному загальному параметру. У цьому випадку рівняння зв'язку компонент деформацій і напруг для пружно-пластичного стану мають вигляд

ε_х – ε_ср = (3/2)(ε_и/σ_и)(σ_x – σ_cp),

………………………………γ_zx = 3(ε_и/σ_и)τ_zx.

    Оскільки приймається, що об'єм в результаті пластичної деформації (після зняття навантаження) не змінюється, то ε_ср = 0 (умова нестисливості).

При простому навантаженні рішення, отримані виходячи з теорії плину та теорії малих пружно-пластичних  деформацій, збігаються. У реальних процесах ОМТ через нерівномірність деформації просте навантаження не реалізується. Рішення, отримані для складного навантаження з використанням названих теорій, дещо різні. Для рішень, в яких визначаються тільки напружений стан, ніякої відмінності в постановці задач немає.

У разі холодної деформації в рівняння пластичності необхідно підставляти значення напруги плину σ_т, отримане за кривими зміцнення (див. гл.6), а для більш точних рішень визначати σ_т, з урахуванням основних факторів, від яких вона залежить, перш за все, температурного поля, поля швидкостей деформацій і власне деформацій. Облік названих чинників необхідний для розгляду процесів гарячої деформації.

Значення σ_т змінно в кожній точці в зоні деформації, а для нестаціонарних процесів змінюється в процесі деформації, що сильно ускладнює його визначення за об’ємом і в часі, З іншого боку, незалежно від розподілу σ_т, завдяки суцільності металу відбувається вирівнювання течії і усереднення тисків на контакті. Тому в багатьох випадках функцію фактичного розподілу σ_т замінюють його середнім значенням за об’ємом і в часі.

Рішення системи з 15 рівнянь, частина з яких задана в диференціальному вигляді, а частина - як лінійні функції, дуже складне і вимагає громіздких викладок. Тому частіше вирішують задачу у спрощеній постановці - плоскій і осесиметричній. При великих деформаціях, що перевищують 5.. 10%, відбувається суттєве відхилення від закону Гука і використовувати фізичні рівняння (зв'язок деформацій і напруг) некоректно. Рішення може обмежуватися визначенням лише компонент напружень або деформацій, або навіть тільки середніх значень компонент, наприклад, середніх значень нормальних напружень, нормальних до поверхні контакту з інструментом (середніх тисків), якщо це відповідає вимогам практики. Рішення значно спрощується, якщо відомо положення головних осей, і не потрібно визначення компонент дотичних напруг і зсувних деформацій. Визначення положення головних осей можливо, якщо відомо, де діють максимальні за абсолютною величиною нормальні напруги.

Рішення, засновані на суттєвих припущеннях і спрощення, називають інженерними. Експериментальна перевірка отриманих рішень показує, що розрахунки з інженерним рішенням часто забезпечують результати, що збігаються з теоретичними рішеннями.

Лекція 10

Визначення поля напружень при осаді смуги в паралельних бойках (задача Прандтля)

 

Один з найбільш поширених методів рішення пластичних задач полягає у вирішенні системи статичних рівнянь рівноваги. Зазвичай цим методом вирішують плоскі і осесиметричні задачи. Розглянемо метод стосовно до процесу осаді смуги в паралельних бойках (Рис.28). Вперше задача вирішена Л. Прандтлем.

Рішення проводимо в довільній прямокутній системі координат. Приймемо, що довжина смуги в напрямку осі y досить велика в порівнянні з висотою h і шириною b. У цьому випадку деформацією по цій осі можна знехтувати. Тому задача є плоскою деформованою, зменшення висоти по осі z відповідає збільшення розміру по осі х, по осі у розмір не змінюється.

 

Рис.28. Осадка смуги

в паралельних бойках

        

Початок координат вибираємо в центрі поперечного перерізу зразка і вирішуємо задачу для його правої верхньої чверті. Сили тертя зумовлюють появу дотичних напружень, спрямованих проти позитивного напрямку х (проти напрямку зміщення точок у правій частині перетину).

У диференціальних рівняннях рівноваги (68) і рівнянні пластичності для плоскої деформованої задачи (102) дотичні напруги запишемо без індексів (для спрощення записів) τ_xz = τ_zx = τ.

Маємо систему з двох рівнянь рівноваги і рівняння пластичності, що включає три невідомі компоненти - σ_x, σ_z, и τ.

    ∂σ_x/∂x + ∂τ /∂z = 0;                                                              (а)

      ∂τ /∂x +∂σ_z/∂z = 0;                                                              (б)

                (σ_x - σ_z)²  + 4τ² = 4k².                                                         (102)

Система статично визначна. Диференціальні рівняння рівноваги позначаємо літерами, так як в рішенні вони використовуються окремо.

Продиференціюємо рівняння (а) за ∂z, а рівняння (б) за ∂x

     ∂²σ_x/∂x∂z + ∂²τ /∂z² = 0;                                                      (в)

      ∂²τ/∂x² +∂²σ_z/∂z∂х = 0.                                                       (г)

Віднімемо другий результат з першого

    ∂²σ_x/∂x∂z - ∂²σ_z/∂z∂х + ∂²τ /∂z² - ∂²τ /∂х² = 0.

    Групуємо  доданки

    (∂²/∂x∂z)(σ_x - σ_z) + ∂²τ/∂z² - ∂²τ/∂х² = 0.                                      (д)

    З рівняння (102) маємо

                  σ_x - σ_z = ± 2 .                                                     (102,а)

Підставляючи значення (σ_x - σ_z) в рівняння (7.1), отримуємо

    (∂²/∂x∂z)(± 2 ) + ∂²τ/∂z² - ∂²τ/∂х² = 0.                          (е)

    Рівняння (е) містить тільки одне невідоме τ. Проте вирішити це диференціальне рівняння другого порядку без додаткових обмежень не можна, так як невідомі значення постійних величин, які звертаються в нулі при першому чи другому диференціюванні. Приймемо допущення, що дотичні напруження на площадках х і z не залежать від координати х (площадка у - головна, на ній дотичні напруження відсутні). Тоді похідні по координаті х у рівнянні (е) звертаються в нулі, звідки отримуємо, що ∂²τ/∂z²=0. Отримане рівняння справедливо, якщо перша похідна ∂τ/∂z=С₁, де С₁ - постійна величина. Поділяючи змінні та інтегруючи ліву і праву частини отриманого рівняння, маємо ∫∂τ=∫С₁∂z, звідки τ=С₁zС₂, де С₂-друга довільна постійна. Знайдемо значення С₁ і С₂ з граничних умов (звертаючись до тих точк, де значення τ відомо).

Внаслідок симетрії тіла горизонтальна осьова площина х₀у є головним площадкаом, на ній дотичне напруження дорівнює нулю. Ця площина характеризується значенням ординати z=0. Значить, при z=0 τ=0, звідки С₂=0. Знайдемо постійну С₁. Нехай на контакті величина дотичних напружень дорівнює - τ_к (знак мінус враховує напрямок дотичних напружень). Контактна площадка характеризується ординатою z= h/2 (див. Рис.28). Тоді - τ_к= С₁h/2, звідки С₁ =-2τ_к/h. У результаті отримуємо рівняння для розрахунку дотичного напруження в будь-якій точці правій верхній чверті смуги

                                      τ = - 2τ_кz/h.                                           (110)

    Як і було прийнято, дотичні напруги не залежать від координати х і зберігають постійне значення на будь-якій горизонтальній площадці.

Для визначення нормальних напружень підставимо значення τ з умови (110) в рівняння (а) і (б)

         ∂σ_x/∂x – ∂(2τ_к z/h)/∂z = 0;                                                      (ж)

      ∂(- 2τ_к z/h)/∂x +∂σ_z/∂z = 0;                                                     (з)

    Отримаємо з рівняння (ж)

               ∂σ_x/∂x – (2τ_к/h)∂z/∂z = 0, чи після скорочення на ∂ z і розділення змінних

                                 ∂σ_x = (2τ_к/h)∂х.

    Интегруємо

                                    ∫∂σ_x = ∫(2τ_к/h)∂х,       

                                   σ_x = (2τ_к/h)х + С₃ + φ₁(z).               (111)

Як завжди при інтегруванні, отримуємо невідому постійну C₃. Крім того, необхідно передбачити наявність невідомої функції φ₁ (z), яка, як і C₃, могла зникнути в результаті диференціювання за ∂х. Звернемося до рівняння (з); його перший доданок звертається в нуль, так як дифференцируєма функція не залежить від х. Отримуємо ∂σz /∂z =0, звідки після відокремлення змінних та інтегрування

                                 σ_z = С₄ + φ₂(х).                                   (112)

Як і в попередньому випадку, отримуємо вже четверту в цьому рішенні невідому постійну С₄ і невідому функцію φ₂ (х), яка повинна була звернутися в нуль при диференціюванні по ∂z.

Для визначення виду невідомих функцій φ₁ (z) і φ₂ (х) використовуємо рівняння пластичності. Підставимо значення σ_х з рівняння (111) і σ_z з рівняння (112) в рівняння (102, а)

(2τ_к/h)х + С₃ + φ₁(z) - С₄ - φ₂(х) = ± 2 , чи

(2τ_к/h)х + С₃ + φ₁(z) - С₄ - φ₂(х) – (± 2 ) = 0.              (113)

Рівняння (113) повинно виконуватися в будь-якій точці правій верхній чверті осередку деформації, тобто за будь-яких значеннях і будь-яких поєднаннях координат х і z в цій чверті. Це можливо в тому єдиному випадку, якщо воно тотожнє дорівнює нулю, тобто коли воно звертається в нуль при будь-яких значеннях і поєднаннях х і z. Ця умова виконується, якщо відомі функції з даної координати рівні невідомій функції з тієї ж координати, взятими зі зворотним знаком. Тоді функції взаємно знищуються. Якщо С₃=С₄=С, то ліва частина рівняння (113) завжди звертається в нуль, умова пластичності виконується в будь-якому випадку. Таким чином

φ₂(х) = (2τ_к/h)х, φ₁(z) = ± 2(k² – τ²)^0,5 = ± 2[k² - (τ_к/h)²z²]^0,5.

Знак ± перед коренем відкидаємо, тому що надалі виберемо потрібний знак з логічних міркувань.

Підставляючи значення φ₁(z) і φ₂(х) в рівняння (111) и (112), отримаємо

σ_x = (2τ_к/h)х – {2[k² - (τ_к/h)²z²]^0,5} + С.                                         (114)

         σ_z = (2τ_к/h)х + С.                                                                             (115)

    Визначимо довільну постійну С. На вільній бічній поверхні смуги напруги, нормальні до цієї поверхні, відсутні. Отже, при  х=b/2 и z =0 σ_x=0, звідки

    0 = (2τ_к/h)(b/2) – 2{2[k² - (τ_к/h)²z²]^0,5} + С. С = - (2τ_к/h)(b/2) – 2k.

    Підставляючи отримане значення С в рівняння (111) і (112), отримаємо

    σ_x = (2τ_к/h)х – {2[k² - (τ_к/h)²z²]^0,5} - (2τ_к/h)(b/2) – 2k.              (116)

         σ_z = (2τ_к/h)х - (τ_к/h)(b) – 2k.                                                 (117)

    При х = b/2 σ_z = – 2k. Так як напруга σ_z стискуюча, то знаки обрані правильно. Виносячи мінус за дужки (він показує, що напруга, що стоїть у дужках, стискуюча) отримуємо остаточно після перетворень

    σ_x = - {2k +τ_к(b/2 - х) – {2[k² - (τ_к/h)²z²]^0,5,                                     (118)

         σ_z = - {2k +τ_к(b/2 - х)}.                                                          (119)

Рівняння (110), (118), (119) дозволяють визначити всі компоненти напружень в будь-якій точці правій верхній чверті смуги. Для лівої верхньої чверті розподіл напруг буде симетрично правій щодо осі z, а напруги в нижній половині - дзеркальним відображенням верхньої. Напруження σ_у рівні напівсумі σ_х і σ_z.

Розподіл напружень σ_z по контакту (епюра тисків) показано на Рис.29. На краях смуги (при х = b/2) σ_z = - {2k + τ_к[(b/2) - (b/2)]} = - 2k. Величина 2k, що характеризує механічні властивості металу, утворює підставу епюри тисків. У напрямку до середини смуги тиску зростають по прямій лінії, так як σ_z залежить тільки від координати z в першому ступені, утворюючи два трикутники. Максимальну величину напруги σ_z (тиску) мають в центрі смуги при х = 0

          σ_z = - {2k + τ_кb/2 - 0} = - {2k + τ_кb/2}.

   

Рис.29. Епюри напружень за об’ємом металу при осаді

 

Чим більше ширина контакту і чим менше висота смуги, тим вище тиск. Для кожного горизонтального перерізу від контакту до площини симетрії х0у вздовж осі z епюра напружень σ_z має постійний вид, так як σ_z не залежить від координати z. З боку нижнього контакту діє така ж епюра тисків, урівноважує верхню епюру.

Епюра напружень σ_х, як випливає з формули (118), має параболічну форму, так як σ_х залежить від z². Напруження σ_х збільшуються від вільної поверхні до вертикальної осі симетрії (Рис.29). Наявність напруг σ_х на вільній поверхні викликано допущенням про незалежність дотичного напруження від координати х. У реальному процесі ці напруги повинні знижуватися до нуля на краях перетину смуги.

Епюра дотичних напружень, як видно з формули (110), для будь-якого вертикального перерізу має постійну форму у вигляді трикутника, на контакті τ=-τ_к, на горизонтальній осі симетрії (на головній площадці) τ=0.

 

Лекція 11

Визначення поля напружень при роздачі товстостінній труби. Метод ліній ковзання

 

Розглянемо товстостінну трубу, що знаходиться під внутрішнім тиском (Рис.30). На практиці це може бути газопровід або трубка, по якій впорскується паливо в циліндр двигуна і т.д. Приймаємо, що довжина труби велика і деформацією по її довжині нехтуємо. У цьому випадку задача стає плоскою деформованою.

Рис3.30. Товстостінна труба

під внутрішнім тиском

 

Так як деформується тіло обертання, і навантаження прикладена симетрично щодо осі симетрії, задача є осесиметричною. Задачу вирішуємо в циліндричній системі координат. Для плоскої задачі вісь z є головною, для осесиметричної задачі головною є вісь θ. Оскільки дві осі - головні, третя вісь ρ також головна (при наявності однієї головної осі положення двох інших головних осей залишається невизначеним).

Таким чином, прийнята циліндрична система координат для даних умов є головною системою, дотичні напруги на її площадках відсутні. Перше з системи диференціальних рівнянь системи (73) набуває вигляду

∂σ_ρ/∂ρ + (σ_ρ - σ_θ)/ρ = 0.                                             (120)  

    Друге рівняння системи (73) для вирішення задача не потрібно. Воно показує, що σ_z є постійною величиною, тому що приводиться до вигляду ∂σ_z=0. Дійсно, для плоскої задачі σ_z=(σ_ρ σ_θ)/2=σ_ср. Рівняння (120) містить дві невідомі σ_ρ і σ_θ. Для вирішення необхідно додати ще одне рівняння. Таким рівнянням є необхідне для вирішення рівняння пластичності. Використовуємо рівняння пластичності для плоскої деформованої задачи в головних осях (103) σ₁-σ₃ = 2k. Оскільки σ_z = σ_ср = σ₂, необхідно вирішити, яке з решти головних напружень найбільше. Напруження σ_ρ здійснюють процес, вони максимальні за абсолютною величиною, але так як вони стискають, то слід прийняти σ_ρ = σ₃. Значить σ_θ = σ₁, а рівняння пластичності приймає вигляд

                            σ_θ  - σ_ρ = 2k.                                                    (121)

    Підставляємо значення σ_θ - σ_ρ в рівняння (120)

                  ∂σ_ρ/∂ρ = - (σ_ρ - σ_θ)/ρ = 2k/ρ.

    Поділяємо змінні та інтегруємо

    ∂σ_ρ = (2k/ρ)∂ρ,  ∫∂σ_ρ = ∫ (2k/ρ)∂ρ, σ_ρ = 2k lnρ + C.

    Знаходимо довільну постійну С з граничних умов. На вільній зовнішньій поверхні труби не можуть діяти напруги, нормальні до цієї поверхні. Отже, при ρ = R σ_ρ = 0, звідки  

0 = 2k lnρ + C, С = - 2k lnR. σ_ρ = 2k lnρ - 2k lnR, σ_ρ = 2k ln(ρ/R)

    Остаточно

                            σ_ρ = - 2k ln(R/ρ).                                             (122)

    Труба повністю перейде в пластичний стан при ρ=r, максимальне значення напруги σ_ρ=-2k ln (R/r). Мінус вказує, що напруга σ_ρ - стискуюче.

У процесі внутрішнього тиску збільшення внутрішнього радіусу випереджає збільшення зовнішнього радіусу, умова (122) є критичне значення внутрішнього тиску, при досягненні якого буде відбуватися роздача труби аж до її руйнування (за умови, що σ_ρ буде залишатися постійним або збільшуватися та без урахування зміцнення матеріалу, тобто при k = пост).     

 

Лекція 12

Метод ліній ковзання

Для використання диференціальних рівнянь рівноваги необхідно звертатися до граничних умов для визначення довільних постійних. Однак не завжди відомо положення меж осередка деформації, не завжди процеси є симетричними щодо хоча б однієї осі. Для вирішення складних завдань у плоскій і осесиметричної постановці з незаданими межами зони деформації використовується метод ліній ковзання. Він може бути використаний і для вирішення простих задач, поля напруг яких визначаються і з допомогою інших методів.

Метод заснований на наступних положеннях. Через кожну точку тіла, що деформується а₁ проходять по дві ортогональні діагональні площадкаи 31 і 13, на яких діють максимальні дотичні напруження τ₃₁ = τ₁₃ = τ_max = k. На цих же площадках діють нормальні напруження σ₃₁ = σ₁₃ = σ_ср. У сусідній точці а₂ також розташовуються діагональні площадкаи 31 і 13, однак їхнє становище дещо відрізняється від положення площадкаів в попередній точці. Діагональні площадкаи і головні дотичні напруги на них будуть постійно змінювати своє положення при переході від точки до точки. Проекції поверхонь, дотичних до діагональних площадок (огинають діагональні площадки), називають лініями ковзання (рис.31). Їх розглядають тільки в пластичній області, в пружних зонах значення напруг на діагональних площадках τ_max <k.

Через кожну точку тіла можна провести дві ортогональні лінії ковзання, які будуть безперервно змінювати своє положення при переході від точки до точки до кордонів пластичної зони. Оскільки лінії ковзання можна розглядати в будь-якій точці пластичної зони і продовжувати у двох взаємно перпендикулярних напрямках, лінії ковзання утворюють два сімейства, які зазвичай позначають α і β. Розглядаючи точки на деяких, не заданих жорстко відстанях один від одного, отримують сітку ліній ковзання, що складається з двох ортогональних сімейств (Рис.32). Точки перетину ліній двох сімейств називають вузловими точками. Метод ліній ковзання вимагає, щоб величина k залишалася сталою для всього осередку деформації.

 

 

Рис. 3.31. Вектори максимального дотичного напруження	Рис.32. Два сімейства         ліній ковзання

 

Розглянемо можливість визначення напруженого стану точки, якщо відомо положення ліній ковзання, що проходять через дану точку а. Позначимо через α_а кут між віссю х і дотичної до лінії сімейства α, проведеної в довільній точці а. Виділимо прямокутний трикутник bcd, гіпотенуза якого лежить на дотичній до лінії ковзання α (рис.33). Трикутник bcd розглядаємо як поперечний переріз призми, протяжність якої уздовж осі у дорівнює одиниці. На катеті bc діють напруги σ_z і τ_xz, на катеті bd - відповідно σ_x і τ_zx, на гіпотенузі, яка є діагональної площадкаом – σ_ср і k.

 

Рис. 33. Схема до висновку основного рівняння для розрахунку напружень з допомогою методу ліній ковзання

 

Розмір вздовж осі у не має значення, так як він увійде співмножником в усі складові рівнянь рівноваги і скоротиться.

Нехай площа грані cd дорівнює F, тоді площа грані bc складе Fcosα_a, а грані bd - Fsinα_a. Розглянемо суму проекцій сил на нормаль N, проведену до межі cd. Приймаємо, що проекції сил, спрямованих по нормалі, позитивні, а спрямованих протилежно - негативні. Для спрощення запису опустимо індекси у попарно рівних дотичних напружень, і кут α_а позначимо просто α.

   σ_cpF + τcosα Fsinα – σ_zcosα Fcosα - σ_xsinα Fsinα + τsinα Fcosα = 0.

    Скорочуючи на F і перетворюючи, маємо

     σ_cp = σ_zcos²α + σ_xsin²α – τsin2α.                                                   (123)

    Візьмемо першу похідну рівняння (123) за ∂α. Вона характеризує зміну середнього нормального напруження вздовж лінії α.

    ∂σ_cp/∂α = - 2σ_zcosα sinα + 2σ_xsinα cosα - 2τcos2α;

    ∂σ_cp/∂α = (σ_х - σ_z)sin2α - 2τcos2α.                                                  (124)

    Висловимо величини σ_х, σ_z і τ через значення σ_ср і k. Для цього розглянемо рівновагу прямокутного трикутника (призми) abc (рис.33), у якого катети є дотичними до ліній ковзання α і β. Складемо рівняння рівноваги сил, що діють на призму одиничної довжини вздовж осей х і z. Попередньо приймемо, що площа грані cb (гіпотенузи) дорівнює F, тоді площа грані ас складе Fcosα, а межі ab - Fsinα.

  ΣX = τF + σ_cpsinα Fcos – σ_cpcosα Fsinα + kcosα Fcosα – ksin Fsinα = 0;

  ΣZ = σ_zF + ksinα Fcosα - σ_cpcosα Fcosα - σ_cpsin Fsinα + kcosα Fsinα = 0.

    Скорочуючи на F і перетворюючи, отримуємо

                  τ = k(sin²α – cos²α) = - kcos2α.                                      (а)    

        σ_z = σ_cpcos²α + σ_cpsin²α – 2kcosα sinα = σ_cp – ksin2α.                     (б)  

    Напруга σ_х знайдемо з умови σ_cp = (σ_x + σ_z)/2, звідки

    Σσ_x = 2σ_cp – σ_z = 2σ_cp - σ_cp + ksin2α = σ_cp + ksin2α.                             (в)

    Підставляючи значення σ_x, σ_z і τ з рівнянь (а), (б) і (в) в рівняння (124), отримуємо

∂σ_cp/∂α = (σ_cp + ksin2α - σ_cp + ksin2α)sin2α + 2kcos2α cos2α =

= 2ksin²2α + 2kcos²2α = 2k.

Отримали диференціальне рівняння з відокремлюваними змінними

                                   ∂σ_cp = 2к∂α.                                              

Якби рішення проводилося для лінії ковзання сімейства β, то в рівнянні з'явився знак мінус:         ∂σ_cp = - 2к ∂α.

У загальному випадку

                                    ∂σ_cp = ± 2к ∂α.                                        (125)

Інтегруя, отримаємо:

                            σ_cp = ± 2к α + С + φ(β),

де невідома функція φ (β) характеризує зміну середньої напруги вздовж лінії ковзання сімейства β, а С - довільна постійна. Рівняння пластичності в даній задачі має вигляд τ=k, воно задовольняється в будь-якій точці, використовувати його для визначення φ (β) неможливо. Для вирішення візьмемо на одній і тій же лінії ковзання сімейства α точки M і N (Рис.34)

Рис.34. Кут повороту лінії

ковзання при переході

від точки M до точки N

 

Для кожної точки отримаємо відповідно

   σ_{ср M} = ± 2к α_M + С + φ(β), (M)

    σ_{ср N} = ± 2к α_N + С + φ(β).  (N)

При русі вздовж лінії ковзання одного сімейства функція φ (β), що залежить від розташування лінії ковзання іншого сімейства, а також довільна постійна не змінюються. Тому, віднімаючи рівняння (N) з рівняння (M), отримуємо

                           σ_{ср M} - σ_{ср N} = ± 2к(α_M - α_N).                                    (126)

    Різницю кутів α_M і α_N позначимо ω_MN (Рис.34). Тоді

                                σ_{ср M} - σ_{ср N} = ± 2кω_MN.                                                               (127)

           Рівняння (127) будемо називати рівнянням ліній ковзання. З нього випливає, що при русі з однієї точки в іншу, що лежить на тій же лінії ковзання, середня напруга змінюється прямо пропорційно куті повороту лінії ковзання між цими точками (куту між дотичними, проведеними в цих точках), а коефіцієнт пропорційності дорівнює 2k. Знак правої частини визначають, виходячи з порівняння значень σ_срM і σ_срN (виходячи з того, збільшується чи зменшується їх різниця при переході від точки M до точки N).

Середня напруга зазвичай легко визначається на вільній поверхні тіла. Для визначення середньої напруги в будь-якій іншій точці (зазвичай вона береться на контактній поверхні) по рівнянню (127) потрібно знайти кут повороту лінії ковзання. Його можна знайти, якщо відомо положення ліній ковзання в осередку деформації. Тому задача зводиться до побудови сітки ліній ковзання. Лінії цієї сітки повинні мати аналітичне подання (повинні бути геометричними кривими, що володіють необхідними властивостями). Побудова сітки ліній ковзання може грунтуватися на наступних міркуваннях. Геометричне місце найбільшого зближення кривих одного і того ж сімейства (характеристичних точок) утворює одну або кілька кривих, які називаються характеристиками цього сімейства. Характеристика або складається з особливих точок кривих цього сімейства, або є обвідної цих кривих, або комбінацією тих і інших точок. Аналіз показує, що лінії ковзання є характеристиками диференціальних рівнянь рівноваги для плоскої задачі. Тому метод називають також методом характеристик. Рівняння характеристик в диференціальній формі мають вигляд

                 dz/dx = tgα и dz/dx = - ctgα.                                  (128)

    Якщо позначити α = 0,5(η – ξ) и β = (η + ξ), то рівняння характеристик можна виразити в параметричній формі у вигляді х=f₁(ξ,η) і в=f₂(ξ,η). Рішення останніх рівнянь теоретично дозволяє знайти положення ліній ковзання, однак досягти остаточного рішення можна тільки в деяких окремих випадках. Найчастіше сітку ліній ковзання будують, грунтуючись на їх властивості та використовуючи типові (стандартні) поля ліній ковзання. Іноді використовують наближені методи побудови сітки.

 

Лекція 13

Властивості і типові поля ліній ковзання. Визначення поля напружень у товстостінній трубі за допомогою методу ліній ковзання.