Тема 3. Симплексний метод розв’язання задач лінійного програмування

Перша праця по лінійному програмуванню була надрукована Канторовичем у 1939 році, але лише після відкриття Данцігом у 1949 році симплекс-метода розв'язання задачі лінійного програмування до цього класу задач виникла зацікавленість. Симплекс-метод дає аналітичний розв’язок лінійної задачі математичного програмування.

Симплексний метод розв’язання задачі лінійного програмування ґрунтується на переході від одного опорного плану до іншого таким чином, що кожного разу значення цільової функції зростає (за умов, що задача має оптимальний план, та кожний з опорних планів не є надмірним). Під опорним планом мають на увазі невід’ємний базисний розв’язок задачі лінійного програмування. Нагадаємо – базисний план (розв’язок) – рішення системи обмежень. у якому усі вільні змінні дорівнюють нулеві, тобто геометрично базисний план відповідає одній з вершин або граней многокутника розв’язків.

Розглянемо використання симплекс-методу для вирішення задачі лінійного програмування на прикладі задачі про планування випуску продукції малим підприємством. У зв’язку з тим, що ця задача була розв’язана раніше, і ми з’ясували, що функціональні планові обмеження виконуються автоматично, а також з метою спрощення пошуку, розглянемо тільки функціональні обмеження ресурсів.

х₁ + 3,5 х₂ £ 350;

2 х₁ + 0,5 х₂ £ 240;

х₁ + х₂ £ 150;

х₁ ³ 0;

х₂ ³ 0.

Z = f (x) = 10 x₁ + 20 x₂ ; Z ® max;

(-Z = - f (x) = - 10 x₁ - 20 x₂ - 0 × x₄ - 0 × x₅; ® min).

Розв’язок задачі. Перетворимо функціональні обмеження-нерівності на обмеження-рівності шляхом введення у обмеження-нерівності невід’ємних вільних невідомих y₁, y₂, y₃ (хоча можливо було б і х₃, х₄, х₅).

 

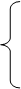х₁ + 3,5 х₂ + у₁ = 350; (1)

2 х₁ + 0,5 х₂ + у₂ = 240; (2)

х₁ + х₂ + у₃ = 150; (3)

 

х₁ ³ 0; х₂ ³ 0; у₁³ 0; у₂³ 0; у₃³ 0.

Перед початком виробництва х₁ = х₂ = 0, тоді

у₁ = 350; наявність ресурсу – шерсть;

у₂ = 240; наявність ресурсу – шовк;

у₃ = 150; наявність ресурсу – трудомісткість.

Прибуток на початок справи Z = 10 × 0 + 20 × 0 = 0;

Кількість рівнянь-обмежень m = 3; кількість невідомих – х₁, х₂, у₁, у₂, у₃ n = 5; кількість вільних змінних – (n – m) = 5 – 3 = 2;

базисне припустиме рішення задачі – це таке, у якому усі вільні змінні дорівнюють нулеві (вершина або грань многокутника розв’язків). Тому початковий опорний план складає

х (1) = (0; 0; 350; 240; 150); Z (х(1)) = 0;

де: х₁ = 0; х₂ = 0 – вільні змінні, відповідає рішенню задачі, коли продукція не виробляється. Надамо цю інформацію у вигляді симплекс-таблиці

 

Таблиця

х1	х2	х3
1 2 1	3,5 0,5 1	350 240 150	у1 – шерстяна тканина у2 – шовкова тканина у3 – наявність ресурсів праці
10	20	0	- Z = - дохід від виробництва

 

Z = 10х₁ + 20х₂ = 10 × 0 + 20 × 0 = 0; - Z = 0;

Виробництво чоловічих костюмів х₂ дає більший дохід, так почнемо його збільшувати, залишаючи х₁ = 0, але існують обмеження. З першої строки симплекс-таблиці (першого рівняння-обмеження на наявність шерстяної тканини) чоловічих костюмів можливо виготовити 350 / 3,5 = 100; з другої строки симплекс-таблиці (другого рівняння-обмеження на наявність шовкової тканини) чоловічих костюмів можливо виготовити 240 / 0,5 = 480 штук; з третьої строки симплекс-таблиці (третього рівняння-обмеження на наявність ресурсів праці) чоловічих костюмів можливо виготовити 150 / 1 = 150 одиниць. Визначальним є обмеження на шерстяну тканину, тобто найбільша кількість чоловічих костюмів (за умов відсутності жіночих – х₁ = 0) дорівнює найменшому з трьох значень 100; 480; 150; х₂ = 110. Визначальний елемент симплекс-таблиці – коефіцієнт у першому рівнянні при другій вільній змінній (х₂), який дорівнює3,5; та має назву центру (ключового елемента).

Як буде виготовлено 100 чоловічих костюмів, так х₂ = 100 і з першого рівняння-обмеження отримаємо (х₁ = 0)

 

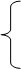у₁ = 350 – 3,5х₂ – х₁; (1)

у₂ = 240 – 0,5х₂ – 2х₁; (2)

у₃ = 150 – х₂ – х₁; (3)

 

що у₁ = 0, тобто ресурсів шерстяної тканини не буде; з другого рівняння-обмеження отримаємо у₂ = 240 – 0,5 × 100 – 2 × 0 = = 190 м шовкової тканини у запасах; з третього рівняння-обмеження отримаємо у₃ = 150 – 100 – 0 = 50 людино - тижнів трудомісткості у запасах.

Прибуток складає Z = 10 × 0 + 20 × 100 = 2000 грн.; - Z = - 2000.

Цільова функція Z = 10 × х₁ + 20 × х₂ через нові вільні змінні (х₁ = 0; у₂ = 0) має вираз

40 40 40 30

Z = 10 х₁ + 20 х₂ = 10 × х₁ + 2000 - ¾ у₁ - ¾ х₁ = 2000 - ¾ у₁ + ¾ х₁,

7 7 7 7

бо (з першого рівняння-обмеження) маємо:

х₂ = 100 – у₁ / 3,5 – х₁ / 3,5.

Перетворимо систему рівнянь-обмежень, замінюючи х₂ на його вираз:

 

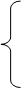х₁ + 3,5 (100 – у₁ / 3,5 – х₁ / 3,5) + у₁ = 350; (1¢)

2 х₁ + 0,5 (100 – у₁ / 3,5 – х₁ / 3,50) + у₂ = 240; (2¢)

х₁ + (100 – у₁ / 3,5 – х₁ / 3,50) + у₃ = 150; (3¢)

х₂ + у₁ / 3,5 + х₁ / 3,5 = 100 (4¢)

 

Другий опорний план задачи таким чином складає

х(2) = (0; 100; 0; 190; 50; 100); Z (х(2)) = 2000;

де: х₁ = 0; у₁= 0 – вільні змінні, відповідає розв’язку задачі, якщо виробляються виключно чоловічі костюми (х₂ = 100). Знов надамо цю інформацію у вигляді симплекс-таблиці.

 

Таблиця

х1	у1	bі
13 ¾ 7	1 - ¾ 7	190	у2 – залишки шовкової тканини
5 ¾ 7	2 - ¾ 7	50	у3 – залишки ресурсів праці
2 ¾ 7	2 ¾ 7	100	х2 – виробництво чоловічих костюмів
30 ¾ 7	40 - ¾ 7	- 2000	- Z – цільова функція

 

Кожен з елементів симплекс-таблиці має своє значення:

– у першому стовпці (х₁) 13 / 7 – потрібна кількість шовкової тканини, потрібної на один жіночий костюм; 5 / 7 – потрібна кількість праці на один жіночий костюм; 30 / 7 – прибуток від одного жіночого костюма;

Дивлячись на цільову функцію

 

30 40

Z = 2000 + ¾ × х₁ - ¾ × у₁,

7 7

 

бачимо, що збільшення виготовлення жіночих костюмів може збільшити прибуток, бо х₁ ³ 0, а також 30 / 7 > 0.

Пригадуючи, що у₁ = 0, знайдемо значення нової вільної змінної, яка задовольняє систему рівнянь-обмежень (2¢), (3¢), (1¢¢), а також у₂ ³ 0, у₃ ³ 0, х₂ ³ 0.

(2¢) дає, якщо у₂ = 0, х₁» 102;

(3¢) дає, якщо у₃ = 0, х₁ = 70;

(1¢¢) дає, якщо х₂ = 0, х₁ =350;

Визначальними є обмеження на ресурси праці:, х₁ = 70, у₃ = 0 з рівняння (3¢).

Визначальний елемент симплекс-таблиці – це коефіцієнт у рівнянні (3¢), якій дорівнює (5/7), та відіграє роль нового центру, або ключового елементу.

Як буде виготовлено 70 жіночих костюмів, так х₁ = 70 з рівняння (3¢) отримаємо у₃ = 0 (нова базова змінна);

Третій опорний план задачі складає:

Х (3) = (70; 80; 0; 60; 0;); Z (3) = 2300 грн.;

Z (3) > Z (1);

де: у₁ = 0; у₃ = 0 - вільні змінні, відповідає розв’язку задачі, якщо виробляється 70 жіночих та 80 чоловічих костюмів. Надамо цю інформацію у вигляді симплекс-таблиці.

 

Таблиця

у3	у1	Опорний розв’язок b1
13 ¾ 5	21 - ¾ 35	60	у2 – залишки шовкової тканини
2 ¾ 5	14 - ¾ 5	80	х2 – кількість чоловічих костюмів
5 - ¾ 7	2 ¾ 5	70	х1 – кількість жіночих костюмів
- 6	28 - ¾ 7	-2300	- Z – цільова функція

 

Збільшити прибуток неможливо у зв’язку з тим, що вільні змінні (у_і > 0), що наявні у цільовій функції мають від’ємні коефіцієнти у той же час, як самі вони додатні. Опорний план Х (3) є оптимальним.

Х* = (х₁* = 70? х₂* = 80; у₁ = 0; у₂* = 60; у₃ = 0);

залишки шовкової тканини складають 60 метрів, прибуток складає 2300 грн., як буде виготовлено 70 жіночих та 80 чоловічих костюмів.

Надамо звичайний вигляд симплекс-таблиці розв’язку задачі.

 

Таблиця 1 ітерація

і	Базисні зміни	х1	х2		х3	х4	х5	bі	Симплекс q = bі / аij	Контроль
1	х3	1 а11	3,5 а12		1 а13	0 а14	0 а15	350	350/3,5=100	355,5
2	х4	2 а21	0,5 а22		0 а23	1 а24	0 а16	240	240/0,5=480	143,5
3	х5	1 а31	1 а32	0 а33		0 а34	1 а17	150	150/1=150	153
4	Z (х)	+10 с1	+20 с2		0 ас3	0 с4	0 с5	0	-	+30

 

Z (х) = (-Z); Z (х) – С₀ – С₁Х₁ – С₂Х₂ – С₃Х₃ – С₄Х₄ – С₅Х₅ = 0;

Z = С₀ + С₁Х₁ + С₂Х₂ + С₃Х₃ + С₄Х₄ + С₅Х₅ = 0 + 10Х₁ + 10Х₂ + 0 × Х₃ + 0 × Х₄+ 0 × Х₅ = 0 × Х₁ + 2 × Х₂ ;

(-Z) = - 10 Х₁ – 20 х₂; ® min

 

Таблиця 2 ітерація

j	Базисні змінні	х1	х2	х3	х4	х5	bi	q = bi / aij	Контроль
1	х2	2 / 7	1	2/ 7	0	0	100	100/(2/7)=350	101 4/7
2	х4	13 / 7	0	-1/ 7	1	0	190	190/(13/7)»102	192 5/7
3	х5	5 / 7	0	-2/ 7	0	1	50	50/(5/7)=70	51 3/7
4	Z (x)	30 / 7	0	-40/ 7	0	0	-2000	-	-2001 3/7

 

х₂ = 100 – (2/7) х₁ – (2/7)х₃; Z (x) + (30/7) х₁ – (40/7)х₃ = -2000;

Z = 10х₁ + 20 × (100 – (2/7)х₁ – (2/7)х₃ ) = 2000 + (30/7)х₁ – (40/7)х₃;

- Z = - 2000 + (40/7)х₃ - (30/7)х₁ = - 2000;

 

Таблиця 3 ітерація

j	Базисні змінні	х1	х2	х3	х4	х5	bi	q = bi / aij	Конт-роль
1	х2	0	1	14/ 35	0	-2/5	80	-	81
2	х4	0	0	21/35	1	-13/5	60	-	59
3	х1	1	0	-2/ 5	0	7/5	70	-	72
4	Z (x)	0	0	-28/ 7	0	-6	-2300	-

 

х₁ = 70 + (2/5) х₃ – (7/5)х₅; Z (x) - (28/7) х₃ – 6 × х₅ = -2300;

Z = 2000 + (30/7) (70 + (2/5)х₃ – (7/5)х₅ ) – (40/7) х₃= 2300 - 6х₅ – (28/7)х₃;

- Z = - 2300 + 6х₅ + (28/7)х₃ = - 2300; х₃ = х₅ = 0.

У цільовій функції усі вільні змінні від’ємні – опорний план Х* = (70; 80; 0; 60; 0) є оптимальним. Задача розв’язана.

 

Z*_max = (-Z*)_min = +2300.

 

Стереометрично ідея методу полягає у тому, що:

- знаходять будь-яку вершину багатогранника розв’язків;

- рухаються вздовж того з ребер, по якому функція зменшується (збільшується) до іншої вершини багатогранника розв’язків;

- як потрапляють у вершину, з якої у всі боки функція зростає (спадає), так знаходять мінімум (максимум).

Нагадаємо ще раз:

- якщо вектор розв’язків задовольняє усім обмеженням, так він має назву плану;

- якщо план відповідає вершині багатогранника розв’язків (усі вільні змінні дорівнюють нулеві), так він має назву опорного плану;

- якщо опорний план відповідає екстремальному значенню цільової функції, так він має назву оптимального плану.

Критерій оптимальності за симплекс-таблицею.

Якщо форма мінімізується (максимізується) і у рідку цільової функції відсутні додатні числа (від’ємні числа), за винятком стовпчика опорний розв’язок (b₁), так опорний план є оптимальним.

Коефіцієнти рядка цільової функції інтерпретують як приріст цільової функції при збільшенні вільної невідомої на одиницю. Приріст додатній, якщо коефіцієнт від’ємний, і навпаки від’ємний, якщо коефіцієнт додатній.

Стовпець “j” є вирішальним, як у цьому стовпцю, оцінка коефіцієнта при невідомій у цільовій функції найбільша за модулем, тобто

 

½ С_j½ = max.

 

Змінну “x_j” у вирішальному стовпцю знаходять за співвідношенням

 

b_i

min ¾ = q, (f_ij > 0; b_i ³ 0);

a_ij

 

яке має назву симплекса, що і дає у свою чергу назву методу. Відповідний елемент a_ij назву ключового елемента, або центру таблиці.

Вільну змінну, яка відповідає вирішальному стовпчику, залучають до базисних змінних, а базисну змінну, яка відповідає мінімальному симплексу, відповідно перетворюють на вільну змінну.

Елементи симплексної строки нової таблиці дорівнюють елементам старої таблиці, поділеним на “ a_ij” – ключовий елемент (центр). Усі інші елементи вирішального стовпця прирівнюють до “0” (за виключенням ключового, якій дорівнює одиниці) шляхом жорданового перетворення; це стосується також цільової функції.

Можливі випадки розв’язку задачі лінійного програмування симплексним методом.

Нескінченна множина оптимальних планів можлива, якщо у строці цільової функції оптимального плану хоча б одна вільна змінна має нульову оцінку (обмеження паралельне цільовій функції). Оптимальне рішення у цьому випадку вирождене, тобто ранг системи рівнянь-обмежень більший за кількість ненульових координат вектора розв’язків.

Необмеженість задачі лінійного програмування виникає, як у якомусь стовпчику змінних у випадку мінімізації “с_j” > 0, а усі елементи таблиці “а_ij” £ 0; у випадку максимізації “с_j” < 0, а усі “а_ij” £ 0. Це позначає, що область припустимих розв’язків задачі не обмежена знизу (мінімізація) або зверхне (максимізація).

Послідовність використання симплекс-методу:

- звести задачу лінійного програмування до задачі мінімізації у канонічній формі (обмеження-рівняння; b_і ³ 0);

- поділити змінні на базисні та вільні і отримати базисне припустиме рішення (базисні змінні невід’ємні; вільні змінні дорівнюють нулеві);

- знайти вираз базисних змінних та цільової функції через вільні змінні;

- за знаком коефіцієнтів при невідомих (с_j £ 0) у цільовій функції з’ясувати, чи є рішення оптимальне

Z = с₀ + с₁х₁ + с₂х₂ + ... + с_nх_n; (c_j ³ 0 – мінімізація); або яку вільну змінну можливо підвищити від нуля та перевести у базис і відповідно, яку базисну змінну перевести у вільні змінні;

- знайти мінімальне додатне співвідношення “b_i” вільних членів рівнянь-обмежень до коефіцієнтів “a_ij” при новій вільній змінній, тобто з’ясувати, яку базисну змінну необхідно перевести у вільні змінні;

- перетворити умови-обмеження та цільову функцію у вираз в залежності від нових вільних змінних.

Приклад.

Розглянемо розв’язання задачі лінійного програмування, якщо у обмеженнях є нерівності двох напрямків. Потрібно максимізувати функцію

 

Z = 4х₁ + 2х₂ – х₃,

 

за умов обмежень

 

х₁ + х₂ + х₃ ³ 8;

х₂ + х₃ £ 10;

х₁ + х₂ + 2х₃ £ 30;

 

Перетворимо першу нерівність за допомогою змінної х₄

 

х₁ + х₂ + х₃ - х₄ £ 8;

 

До цих трьох обмежень додамо штучні змінні у₁, у₂, у₃ (х₅, х₆, х₇). Цільова функція набуває вигляду

 

Z = 4х₁ + 2х₂ – х₃ + 0 × х₄;

 

обмеження:

 

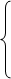х₁ + х₂ + х₃ – х₄ + у₁ + 0 × у₂ + 0 × у₃ = 8;

0 × х₁ + х₂ + х₃ + 0 × х₄ + 0 × у₁ + у₂ + 0 × у₃ = 10;

х₁ + х₂ + 2х₃ + 0 × х₄ + 0 × у₁ + 0 × у₂ + у₃ = 30;

 

Вектори у₁ (0); у₂ (1); у₃ (0) утворюють базис

тримірний у загальному симівимірному просторі х₁, х₂, х₃, х₄, у₁, у₂, у₃.

Кількість невідомих n = 7; обмежень m = 3; вільних змінних n – m = 7 – 3 = 4.

Базові змінні у₁, у₂, у₃; вільні змінні х₁, х₂, х₃, х₄. Базове опорне рішення

 

х (0; 0; 0; 0; 1; 1; 1), Z (х) = 0.

 

Розв’язок задачі надамо у вигляді симплекс-таблиці.

 

Таблиця

і	базисні змінні	х1	х2	х3	х4	у1	у2	у3	bi	q=bi/fij
1	у1	1	1	1	-1	1	0	0	8	8/1
2	у2	0	1	1	0	0	1	0	10	10/1
3	у3	1	1	2	0	0	0	1	30	30/1
4	-Z	4	2	-1	0	0	0	0	0
1	х2	1	1	1	-1	1	0	0	8	-8/1
2	у2	-1	0	0	1	-1	1	0	2	2/1
3	у3	0	0	1	1	-1	0	1	22	22/1
4	-Z	2	0	-3	2	-2	0	0	-16
1	х2	0	1	1	0	0	1	0	10	10/1
2	х4	-1	0	0	1	-1	1	0	2	2/-1
3	у3	1	0	1	0	0	-1	1	20	20/1
4	-Z	4	0	-3	0	0	-2	0	-20
1	х2	0	1	1	0	0	1	0	10	10/1
2	х4	0	0	1	1	-1	0	1	22	22/0
3	х1	1	0	1	0	0	-1	1	20	20/-1
4	-Z	0	0	-7	0	0	2	-4	-100
1	у2	0	1	1	0	0	1	0	10
2	х4	0	0	1	1	-1	0	1	22
3	х1	1	1	2	0	0	0	1	30
4	-Z	0	-2	-9	0	0	0	-4	-120

 

Х* (30; 0; 0; 22; 0; 10; 0); Z = 4х₁ + 2х₂ – х₃ = 4 × 30 = 120.

Z* = 120 – 2х₂ – 9х₃ – 4у₃ = 120.