Дробное рациональное уравнение

Дробно рациональное уравнение - рациональное (без знака корня) уравнение, в котором левая или правая части являются дробными выражениями.

 

Уравнение: 3. Является дробным, так как тут есть деление на переменную x,

 а это говорит о том, что уравнение не целое.

 

Для правильного решения рациональных уравнений, ты должен придерживаться следующего руководства:

1. Понять, точно ли перед тобой рациональное уравнение (убедись, что в нем нет корней);

2. Определить ОДЗ;

3. Найти общий знаменатель дробей и умножить на него обе части уравнения;

4. Решить получившееся целое уравнение;

Исключить из его корней те, которые обращают в ноль знаменатель дробей

 

Биквадратные уравнения

Биквадратным уравнением — называется уравнение вида ax⁴ + bx² + c = 0.

 

 

Биквадратное уравнение приводится к квадратному уравнению при помощи подстановки .

 

Новое квадратное уравнение относительно переменной :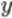

 

 

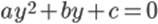
Решая это уравнение, мы получаем корни квадратного уравнения 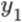 и . Решая эти два уравнения ( и ) относительно переменной , мы получаем корни данного биквадратного уравнения.

Порядок действий при решении биквадратных уравнений

▪ Ввести новую переменную

▪ Подставить данную переменную в исходное уравнение

▪ Решить квадратное уравнение относительно новой переменной

После нахождения корней () подставить их в нашу переменную  и найти исходные корни биквадратного уравнения