2020-05-11
84
Неопределенный интеграл. Задание 1-10
В дифференциальном исчислении решается задача: по данной функции 
найти ее производную или дифференциал. Интегральное исчисление решает обратную задачу: найти функцию 
, зная ее производную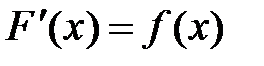 
(или дифференциал 
), т.е. найти такую функцию , производная которой равнялась бы 
.
Определение. Функция называется первообразной функции на интервале 
, если для любого 
выполняется равенство
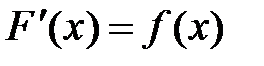или .
Например, первообразной функции 
, 
, является функция 
, т.к. 
. Очевидно, что первообразными будут также любые функции 
, где С - константа, т.к. 
.
Определение. Множество всех первообразных функций 
для называется неопределенным интегралом от функции и обозначается символом 
, т.е. 
,
– подынтегральная функция; 
– подынтегральное выражение;
х – переменная интегрирования; 
– знак неопределенного интеграла.
Свойства неопределенного интеграла.
1. 
(где с – константа, 
) – постоянный множитель можно выносить за знак интеграла.
2. 
– неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от этих функций.
Таблица основных интегралов.
1. 
2. 
(
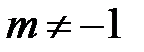). В частности 
.
3. 
4. 
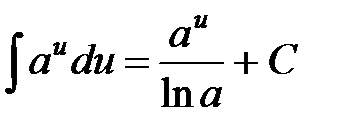
5. 
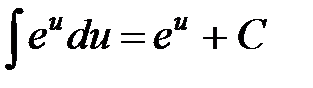
6. 
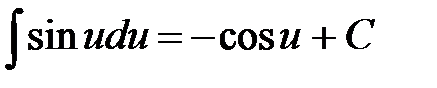
7. 
8. 
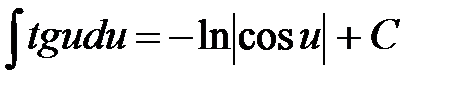
9. 
10. 
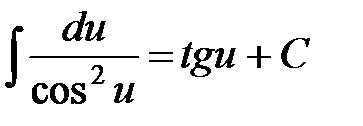
11 
12. 
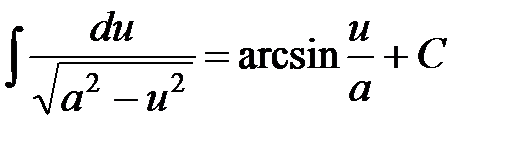. В частности 
.
13. 
. В частности 
.
17. 
В справедливости приведенных формул можно убедиться, взяв производную правой части, которая будет равна подынтегральной функции.
Метод непосредственного интегрирования
Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.
Примеры:
1. 
2. 
.
При сведении интеграла к табличному часто используются следующие преобразования дифференциала (операция «подведение под знак дифференциала»): 
, 
, а и b – числа,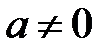 
.
3. 
;
4. 
;
Из приведенных примеров выводим следующее правило интегрирования:
если , то 
, (a,b –числа).
