Произвольная пространственная система сил

7.1. ЛЕММА ПУАНСО О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ СИЛЫ

Рассмотрим теперь самый общий случай — систему, состоящую из любого количества сил, как угодно расположенных в пространстве.

Для краткости будем называть такую систему произвольной пространственной системой сил.

Прежде чем перейти к ее преобразованию, приведем вспомогательную теорему (лемму Пуансо) о параллельном переносе силы.

Луи Пуансо (Louis Poinsot, 1777-1859) — французский математик и механик, автор геометрической статики (1803). Ввел в механику понятия момента силы, пары сил, разработал теорию пар и метод приведения системы сил. Многое сделал в кинематике и динамике.

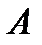Пусть дана сила , приложенная в точке (рис. 7.1а).

Приложим к некоторой точке две силы: и , равные по величине и противоположно направленные (), что допускается в соответствии с аксиомой 2, поскольку .

Рис. 7.1

Пусть по модулю они будут равны силе и параллельны ей (рис. 7.1).

Полученная система сил представляет собой силу , геометрически равную силе , приложенную в центре приведения и пару сил и , момент которой равен .

Поскольку выполненные преобразования эквивалентны, то

Добавляемая пара сил называется присоединенной парой.

Момент присоединенной пары, добавляемой при приведении силы 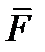к центру , равен моменту данной силы относительно вновь выбранного центра :

Доказана ЛЕММА ПУАНСО:

силу 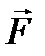можно переносить на параллельную линию действия, добавляя при этом присоединенную пару, момент которой равен моменту силы относительно новой точки приложения силы.

Операция переноса силы в заданную точку называется приведением силы к заданному центру.

7.2. ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ К ПРОИЗВОЛЬНОМУ ЦЕНТРУ

Если рассматривается система сил, то все силы (пользуясь леммой Пуансо) можно привести к некоторому центру. В результате этого исходная система сил упростится.

Рис. 7.2

ОСНОВНАЯ ТЕОРЕМА СТАТИКИ (теорема Пуансо)

Любая система сил при приведении к произвольному центру заменяется одной силой и одной парой. При этом сила равна главному вектору системы сил и приложена в центре приведения, а пара имеет момент, равный главному моменту системы сил относительно центра приведения.

Доказательство

Рассмотрим произвольную систему сил (рис. 7.2., а).

Следуя методу Пуансо, каждую силу системы 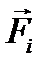приведем к центру О, добавляя (рис. 7.2, б) при каждом переносе присоединенную пару с моментом , который равен моменту данной силы относительно точки О:

Образовавшуюся в точке О систему сходящихся сил (рис. 7.3) заменим одной силой, которая равна главному вектору системы:

(7.1)

Рис. 7.3

Систему присоединенных пар заменим одной парой (рис. 7.3), момент которой равен сумме моментов присоединенных пар и следовательно, равен главному моменту системы сил: