Выберем прямоугольную декартову систему координат на плоскости. Всякое комплексное число
 определяется парой действительных чисел
определяется парой действительных чисел 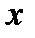 и
и  Поэтому, естественной геометрической интерпретацией комплексного числа
Поэтому, естественной геометрической интерпретацией комплексного числа  является его изображение точкой
является его изображение точкой  плоскости с декартовыми координатами
плоскости с декартовыми координатами  и
и  (рис.1). Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью.
(рис.1). Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью.
Множество всех действительных чисел изображается на оси абсцисс, которая называется действительной осью, а множество всех чисто мнимых чисел-на оси ординат (кроме начала координат), которая называется мнимой осью. Начало координат, которому соответствует число 0=(0,0),называют нулевой точкой.
Для геометрического представления комплексного числа  кроме точки (x,y) используется также вектор, начало которого находится в точке O(0,0), а конец - в точке М(x,y). Здесь следует подчеркнуть, что отмеченное соответствие между множеством всех комплексных чисел и векторами на плоскости позволяет операции сложения и вычитания комплексных чисел
кроме точки (x,y) используется также вектор, начало которого находится в точке O(0,0), а конец - в точке М(x,y). Здесь следует подчеркнуть, что отмеченное соответствие между множеством всех комплексных чисел и векторами на плоскости позволяет операции сложения и вычитания комплексных чисел  и
и 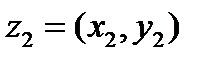 проводит по правилу сложения и вычитания векторов (рис.2).
проводит по правилу сложения и вычитания векторов (рис.2).
Длина вектора, соответствующего комплексному числу  , называется модулем этого числа и определяется формулой
, называется модулем этого числа и определяется формулой
 (1)
(1)
Угол межу этим вектором и положительным направлением действительной оси Ox называется аргументом числа  и обозначается через
и обозначается через 
Для числа  , модуль которого равен нулю, понятие аргумента не имеет смысла, а при
, модуль которого равен нулю, понятие аргумента не имеет смысла, а при  аргумент
аргумент  определяется с точностью до слагаемого кратного 2
определяется с точностью до слагаемого кратного 2  .
.
Среди всех значений  существует одно и только одно значение, лежащее в промежутке
существует одно и только одно значение, лежащее в промежутке  Оно называется главным значением аргумента и обозначается через
Оно называется главным значением аргумента и обозначается через 
Таким образом,
 (2)
(2)
где главное значение аргумента комплексного числа  определяется формулами (рис.1):
определяется формулами (рис.1):
 при
при  ,
,
 при
при  и
и  (3)
(3)
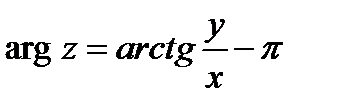 при
при  и
и 
 при
при 
 при
при 
Таким образом, всякое конечное комплексное число  полностью определяется модулем и аргументом этого числа.
полностью определяется модулем и аргументом этого числа.
 2020-05-12
2020-05-12 361
361








