Математическое ожидание

 

(если число возможных значений конечно)

Математическим ожиданием дискретной случайной величины называется величина

 

(если число возможных значений бесконечно, причем, математическое ожидание , если ряд сходится абсолютно)

или

 

 

(так как, ряд может и расходиться, то соответствующая случайная величина может и не иметь математического ожидания)

 

Пример.

					…		…
					…		…

 

 

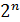
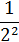
 У этой случайной величины математическое ожидание не существует.

 

Математическое ожидание случайной величины – это неслучайная постоянная величина. Она имеет размерность случайной величины.

Математическое ожидание – это среднее значение случайной величины, центр ее распределения.

Нельзя путать математическое ожидание с наиболее вероятным значением случайной величины.

Неправильно  говорить «среднее ожидаемое».

 

Пример.

Пусть случайная величина Х – число очков на игральной кости. Ее ряд распределения

					4		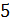6

 

Математическое ожидание Х равно .  

Очевидно, бесполезно ожидать, что на кубике выпадет 3,5 очка.

Пример из механики.

Если массы  расположены в точках с абсциссами , то абсцисса центра тяжести системы материальных точек

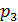
вычисляется по формуле

 

Можно сказать, что математическое ожидание - «средневзвешенное» значение случайной величины.

 

Интерпретация математического ожидания в финансовом анализе.