Независимость случайных величин

Случайные величины

Случайная величина – это переменная, которая в результате испытания принимает одно из своих возможных [числовых] значений, причем заранее неизвестно, какое именно, так как это зависит от случая. Случайные величины обозначаются латинскими буквами , , . Их возможные значения .

Примеры.

Число студентов на лекции. Рост наугад отобранного студента.

Более строго случайная величина определяется как функция, заданная на пространстве элементарных событий (множестве элементарных исходов), то есть f (ω), где – элементарный исход .

Например,

Случайная величина – число дней во взятом наугад месяце года.

, , …

Определение.

Случайной величиной, связанной с данным вероятностным пространством , называется действительная функция , определенная на пространстве элементарных событий W, такая, что для действительного числа множество элементарных событий, для которых выполняется неравенство , является событием (то есть ).

Случайные величины описываются законом распределения вероятностей, то есть соответствием между возможными значениями случайных величин и их вероятностями. Закон распределения имеет различные формы.

Функция распределения вероятностей
(интегральная функция распределения)

Функцией распределения случайной величины называется функция, определенная равенством

Свойства.

Свойство 1. , так как это вероятность.

Свойство 2. – неубывающая функция, то есть если , .

Доказательство.

Пусть .

Событие представляет собой сумму несовместных событий.

(1)

.▄

Свойство 3.

Свойство 4. непрерывна слева в любой точке.

Свойство 5. , (следует из формулы (1), если положить , .)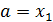

Свойство 6. = x₁равен .

Независимость случайных величин

Две случайные величины называются независимыми, если закон распределения одной из них не меняется от того, какое возможное значение приняла другая случайная величина.

Пусть задана система случайных величин . Будем говорить, что и независимы, если независимы события и , где и – любые два отрезка и .