Дискретные случайные величины

 

Наиболее удобными для изучения являются так называемые дискретные случайные величины. Они характеризуются тем, что их множество возможных значений конечно или счетно.

Закон распределения дискретной случайной величины задается рядом распределения.

 

				…		…	(1)
				…		…

 

Свойство.

Для дискретной случайной величины функция распределения  – это функция ступенчатого типа. Она терпит разрыв в точках  причем имеет в этих точках скачек .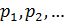

 

1

 

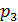
Независимость дискретных случайных величин  и  означает независимость событи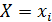й  и , , .

 

.

 

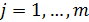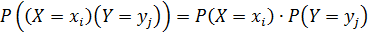Функция от случайной величины

 

Пусть  – случайная величина. Часто возникает необходимость в рассмотрении случайной величины  вида , где  – заданная числовая функция.

Если  – непрерывная функция, то соотношение  определяет случайную величину .

Если закон распределения случайной величины  задан таблицей (1), то закон распределения  задан таблицей

 

				…

 

Если среди  имеются равные, то соответствующие столбцы надо объединить в один столбец, сложив соответствующие вероятности.

 

Пример.

		-2	-1	0	1	2
		0,2	0,2	0,2	0,2	0,2

 

		4	1	0	1	4
		0,2	0,2	0,2	0,2	0,2

 

		0	1	4
		0,2	0,4	0,4

 

Суммой (разностью или произведением) случайных величин  и  называется случайная величина, которая принимает все возможные значения вида  (  или 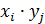), где ,  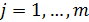с вероятностями .

Если случайные величины  и  независимы, то есть независимы любые события 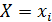, , то по теореме умножения

 

.

 

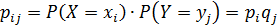Пример.

		0	2	4
		0,5	0,2	0,3

 

		-2	0	2
		0,1	0,6	0,2

 

Найти а) 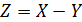, б)

 

 

Числовые характеристики дискретных случайных величин

 

Закон распределения случайной величины дает исчерпывающую информацию о ней. Однако, во многих случаях удобно ограничиться так называемыми числовыми характеристиками.