Вопрос 1. Понятие случайного события и случайного эксперимента.
Предмет теории вероятностей
Теория вероятностей изучает закономерности, возникающие в случайных экспериментах. Случайным называют эксперимент, результат которого нельзя предсказать заранее. Невозможность предсказать результат отличает случайное явление от детерминированного.
Пространство элементарных исходов.
Определение 1. Пространством элементарных исходов 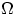 («омега») называется множество, содержащее все возможные результаты данного случайного эксперимента, из которых в эксперименте происходит ровно один. Элементы этого множества называют элементарными исходами и обозначают буквой
(«омега») называется множество, содержащее все возможные результаты данного случайного эксперимента, из которых в эксперименте происходит ровно один. Элементы этого множества называют элементарными исходами и обозначают буквой 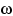 («омега»).
(«омега»).
Определение 2. Событиями мы будем называть подмножества множества 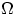 . Говорят, что в результате эксперимента произошло событие
. Говорят, что в результате эксперимента произошло событие  , если в эксперименте произошел один из элементарных исходов, входящих в множество
, если в эксперименте произошел один из элементарных исходов, входящих в множество  .
.
Замечание 2. Вообще говоря, можно назвать событиями не обязательно любые подмножества множества 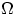 , а лишь элементы некоторого набора подмножеств. О смысле такого ограничения мы поговорим позднее.
, а лишь элементы некоторого набора подмножеств. О смысле такого ограничения мы поговорим позднее.
Определение 3.
1. Достоверным называется событие, которое обязательно происходит в результате эксперимента, т.е. единственное событие, включающее все элементарные исходы — событие 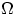 .
.
2. Невозможным называется событие, которое не может произойти в результате эксперимента, т.е. событие, не содержащее ни одного элементарного исхода («пустое множество»  ). Заметим, что всегда
). Заметим, что всегда  .
.
Операции над событиями
В теории вероятностей существуют ровно те же операции над множествами, что и в теории множеств.
Определение 4.
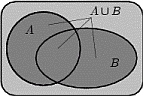

1. Объединением  событий
событий  и
и 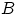 называется событие, состоящее в том, что произошло либо
называется событие, состоящее в том, что произошло либо  , либо
, либо 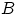 , либо оба события одновременно. На языке теории множеств
, либо оба события одновременно. На языке теории множеств  есть множество, содержащее как элементарные исходы из множества
есть множество, содержащее как элементарные исходы из множества  , так и элементарные исходы из множества
, так и элементарные исходы из множества 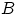 .
.
2. Пересечением  событий
событий  и
и 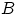 называется событие, состоящее в том, что произошли оба события
называется событие, состоящее в том, что произошли оба события  и
и 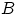 одновременно. На языке теории множеств
одновременно. На языке теории множеств  есть множество, содержащее элементарные исходы, входящие в пересечение множеств
есть множество, содержащее элементарные исходы, входящие в пересечение множеств  и
и 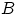 .
.


3. Противоположным (или дополнительным) к событию  называется событие
называется событие  , состоящее в том, что событие
, состоящее в том, что событие  в результате эксперимента не произошло. Т.е. множество
в результате эксперимента не произошло. Т.е. множество 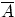 состоит из элементарных исходов, не входящих в
состоит из элементарных исходов, не входящих в  .
.
4. Дополнением  события
события 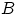 до
до  называется событие, состоящее в том, что произошло событие
называется событие, состоящее в том, что произошло событие  , но не произошло
, но не произошло 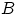 . Т.е. множество
. Т.е. множество  содержит элементарные исходы, входящие в множество
содержит элементарные исходы, входящие в множество  , но не входящие в
, но не входящие в 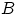 .
.
Определение 5.

1. События  и
и 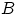 называют несовместными, если
называют несовместными, если  .
.
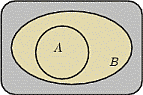
2. События  называют попарно несовместными, если для любых
называют попарно несовместными, если для любых 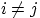 , где
, где  , события
, события  и
и 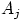 несовместны.
несовместны.
3. Говорят, что событие  влечёт событие
влечёт событие 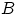 , и пишут
, и пишут  , если всегда, как только происходит событие
, если всегда, как только происходит событие  , происходит и событие
, происходит и событие 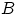 . На языке теории множеств это означает, что любой элементарный исход, входящий в множество
. На языке теории множеств это означает, что любой элементарный исход, входящий в множество  , одновременно входит и в множество
, одновременно входит и в множество 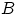 , т.е.
, т.е.  содержится в
содержится в 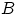 .
.
Вопрос 2. Статистическое определение вероятности
Не все случайные явления (эксперименты) можно изучать методами теории вероятностей, а лишь те, которые могут быть воспроизведены в одних и тех же условиях.
Определение. Вероятностью события A называется число Р(А), около которого колеблется значение статистической частоты этого события при условии увеличения количества испытаний.
При статистическом определении в качестве вероятности события принимается его относительная частота.
Относительной частотой события  называют отношение числа испытаний
называют отношение числа испытаний  , в которых данное событие появилось, к общему числу
, в которых данное событие появилось, к общему числу 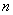 фактически проведённых испытаний:
фактически проведённых испытаний:  .
.
Частота события обладает следующими свойствами:
1. Частота случайного события есть число, заключенное между нулем и единицей:
0<P(A)<1
2. Частота достоверного события U равна единице:
P(U)=1
3. Частота невозможного события V равна нулю:
P(V)=0
4. Частота суммы двух несовместных событий A и B равна сумме частот этих событий:
P(A+B)=P(A)+P(B)
Пример 1. Из 500 взятых наудачу деталей оказалось 8 бракованных. Найти частоту бракованных деталей.
Решение. Так как в данном случае m = 8, n = 500, то в соответствии с формулой находим
P(A)=8:500=0,016
Пример 2. Игральный кубик подброшен 60 раз, при этом шестерка появилась 10 раз. Какова частота появления шестерки?
Решение. Из условия задачи следует, что n = 60, m = 10, поэтому

 2020-05-12
2020-05-12 139
139







