2020-05-12
171
Пусть некая одномерная система с дискретным временем на k -ом шаге характеризуется «состоянием» x (k) и эволюционирует по закону
; (3.4)
a – известный параметр. Соотношение (10.4) называют уравнением динамики системы. Пусть на каждом шаге имеются измерения
(3.5)
с известным параметром h. Соотношение (3.5) называют уравнением измерений. Требуется найти в рекуррентной форме последовательность оценок состояния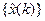 
.
Предположим, что оценка для k -го шага 
уже найдена, при этом известна ее дисперсия 
. Тогда для нахождения 
и ее дисперсии 
имеем следующую систему уравнений:
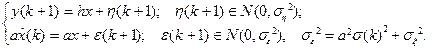
Выровняем эти соотношения так, чтобы дисперсии погрешностей в них стали одинаковыми:
и найдем 
с помощью метода наименьших квадратов:
(3.6)
Приравняем нулю производную 
.
Отсюда
(3.7)
или
. (3.8)
Остается только найти закон изменения дисперсии 
Это легче всего сделать на основе предпоследнего соотношения (3.7):
|
|
|
(3.9)
Это соотношение называют уравнением Рикатти. График изменения дисперсии называют обучающей кривой.
Действительный интерес представляют схемы, в которых параметры 
сами меняются от шага к шагу.
Если а =1 и 
то есть на каждом шаге оценивается постоянный параметр x, получаем рекуррентную схему вычисления коэффициента наклона x в линейной модели
y (k) = x . h (k)+ η(k).
Основной смысл рассмотренной конструкции состоит в том, что она на каждом шаге комплексирует данные, поступающие из двух источников, выдавая оценку, усредненную в соответствии с текущими характеристиками точности этих источников.
3.3. m - мерный линейный фильтр Калмана
Рассмотрим вероятностную динамическую систему, описываемую линейными разностными уравнениями состояний и наблюдений. Уравнение состояний
x (n+ 1) = F(n+ 1 ,n) .x (n) + G(n+ 1 ,n) .w (n+ 1) (3.10)
характеризует динамику системы, уравнение наблюдений
y (n) = H (n) .x (n) + v (n) (3.11)
определяет механизм образования данных, получаемых в процессе измерений.
В уравнениях (3.10) и (3.11)
· x (n) – m -мерный вектор состояния системы;
· F(n+1,n) – ее переходная матрица размерности m ´ m;
· w (n) – случайный k -мерный вектор гауссовых шумов (возмущений) системы с нулевым средним и ковариационной матрицей M[ w (n) wT (j)]= Q (n). d (j,n);
· G (n +1, n) – переходная матрица возмущений системы размерности m ´ k;
· y (n) – s –мерный вектор результатов измерений на n -м шаге;
· H (n) – переходная матрица наблюдений размерности s ´ m;
|
|
|
· v (n) – случайный s -мерный вектор гауссовых шумов измерений с нулевым средним и ковариационной матрицей M[ v (n) vT (j)]= R (n). d (j,n);
· d (j,n) – символ Кронекера.
В этих условиях оптимальная текущая оценка описывается следующими рекуррентными соотношениями:
(3.12)
Матрица Q(n), скорее даже более общая конструкция G(n) Q (n)G T (n), определяет степень неопределенности для уравнения состояний.
При прогнозировании на k шагов вперед используется уравнение состояний (3.10) с переходной матрицей
Наилучшие ситуации здесь возникают, когда матрица F с самого начала задана в виде F(t, t+t).
Ковариационная матрица погрешностей прогноза вычисляется по формуле
Замечание. Если положить в (3.10) F(n+ 1 ,n)= I, G(n+ 1 ,n)=0, то соотношения (3.12) примут вид
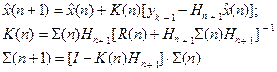
(рекуррентный МНК). В качестве начального приближения 
берется произвольный вектор размерности < r ×1> и, например, матрица uI размерности < r × r > с достаточно большим множителем u.
Варианты определения исходных параметров
Если используется гипотеза о равномерном прямолинейном движении объекта, то его состояние описывается 4-мерным вектором x (t) = [ x, y, vx, vy ] T, а переходная матрица имеет вид
.
Отсюда получается основное соотношение
x (t +t) = F(t) x (t),
или, в координатах,
x (t +t) = x (t) +t vx, y (t +t) = y (t) +t vy, vx (t +t) = vx (t), vy (t +t) = vy (t).
Переходная матрица возмущений системы G в простейших случаях оказывается единичной, а ковариационную матрицу Q следует выбирать достаточно большой, например,
Эти матрицы описывают степень нашей неуверенности в правильности предположения о равномерности и прямолинейности движения. Большое значение Q обеспечивает возможность следить за маневрирующими объектами. Более сложные конструкции Г появляются, если нужно описать коррелированные возмущения.
Если используются прямые измерения, то переходная матрица наблюдений Н оказывается единичной. Если бы на вход системы подавалась информация, например, в виде пеленгов и дальностей, это нашло бы отражение в конструкции матрицы Н.
Более общий вариант возникает, когда динамика системы задана в виде системы дифференциальных уравнений, например,
Решение этой системы с помощью матричной экспоненты на равномерной сетке с шагом τ приводит к соотношениям
Возможны более сложные варианты, когда динамика задана неоднородной системой или системой стохастических дифференциальных уравнений. В этом случае решение системы с помощью матричной экспоненты сразу включает адекватное представление второго слагаемого в (3.10).
Пример. Типичную ситуацию можно представить себе следующим образом. Базовое представление траектории спутника – эллипс. Этим и диктуется задание уравнения динамики. В действительности над, например, месторождением тяжелых металлов спутник летит на несколько десятков метров ниже, над соляным куполом (под такими куполами часто скапливается нефть) - на несколько десятков метров выше. Текущие измерения высоты осуществляются с ошибкой, характеристики которой зависят от условий наблюдаемости. Фильтр комплексирует предполагаемую динамику с текущими измерениями, выдавая на каждом шаге оценку, усредненную в соответствии с заданными характеристиками точности, определяемыми матрицами Q и R.
Контрольные вопросы
- Связь между вычислением среднего и экспоненциальным сглаживанием
- Понятия коэффициента передачи и обновляющего процесса
- Понятия вектора состояний и переходных матриц
- Понятия переходных матриц возмущений и наблюдений
- Уравнение Рикатти и обучающие кривые
- Простейшие варианты задания переходных матриц
- Получение переходных матрицы из мультипликативной процедуры решения систем дифференциальных уравнений
Задания на лабораторную работу № 3
|
|
|
1. Сформировать временной ряд измерений среднего
2. Запрограммировать процесс рекуррентного оценивания среднего
3. Вывести графики временных рядов измерений и оценок и обучающую кривую
4. Сформировать временной ряд измерений коэффициента наклона
5. Запрограммировать процесс рекуррентного оценивания коэффициента наклона
6. Вывести графики временных рядов измерений и оценок и обучающую кривую
