Системы массового обслуживания с ожиданием

Если время ожидания ничем не ограничено, СМО называется «чистой системой с ожиданием». Обычно ожидание ограничено

• Временем ожидания в очереди;
• Общим временем пребывания заявки в системе (если время закончилось, то обслуживание прерывается и заявка считается необслуженной. Пример: цель в зоне поражения;
• Длиной очереди.

Такие СМО называют «системами смешанного типа». Для них рассматривают еще разные варианты «дисциплины очереди». Ожидающие заявки могут приниматься на обслуживание

• В порядке очереди;
• В случайном порядке;
• С учетом приоритетов.

Если все процессы в СМО являются марковскими, ее описание достаточно просто. При наличии сложных ограничений приходится либо непосредственно выписывать систему дифференциальных уравнений для p (t), либо использовать марковскую аппроксимацию и уповать на высокую робастность формул Эрланга.

Сводка основных формул для Марковских СМО

Система с отказами. Обозначим ν = λ/μ; k =0,…, m. Пусть

.

Тогда вероятность того, что в стационарном режиме в системе окажутся занятыми k каналов

Вероятность того, что хоть один канал свободен

Если w – число занятых каналов, то Mw = νP_обсл.

  Система с неограниченной очередью. ν = λ/μ; k = 0, …, m.

                  .

Длина очереди. Обозначим   Пусть

• γ - время ожидания в очереди;
•  - длина очереди – случайная величина.

Тогда     

Потоки с ограниченным последействием (поток Пальма)

Поток однородных событий x (t) называется потоком с ограниченным последействием (потоком Пальма), если он удовлетворяет условию ординарности, а промежутки времени между следующими друг за другом вызовами представляют собой независимые случайные величины. Простейший поток является частным случаем потока Пальма, он отличается тем, что для него время ожидания распределено по показательному закону.

Рассмотрим простейший поток и выбросим из него каждую (k+ 1 ) -ю точку. Тогда оставшиеся точки образуют поток Эрланга порядка k. Это – частный случай потока Пальма.

Формулы Литтла

Как ни удивительно, можно найти целый ряд соотношений, допускающих статистическую трактовку, верных для любых СМО – возможно, немарковских, с произвольным законом формирования очереди) – в установившемся режиме. Пусть

• x (t) – число заявок, поступивших к моменту t;
• y (t) - число заявок, покинувших систему к моменту t;
• z (t) - число заявок, находящихся в системе в момент t;

z (t) = x (t) - y (t). Тогда

 -

- среднее число заявок, находящихся в СМО в единицу времени; Lt - среднее число заявок, обслуженных за время t.  

  Пусть t_i – время обслуживания i -й заявки, тогда

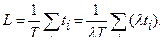
Здесь λ Т – среднее число пришедших заявок;  - суммарное время обслуживания всех заявок,  - среднее время W _сист пребывания заявки в системе. Отсюда

- первая формула Литтла.

  Аналогично, если L _оч - средняя длина очереди, а W _оч – среднее время пребывания в очереди, то

- вторая формула Литтла.

Контрольные вопросы

1. Однородная цепь Маркова с дискретным временем
2. Физическая интерпретация
3. Эргодические теоремы
4. Однородная цепь Маркова с непрерывным временем
5. Уравнения Чепмена-Колмогорова
6. Формулы Эрланга
7. Потоки событий
8. Простейший поток и экспоненциальный закон
9. СМО с отказами
10. СМО с ожиданием
11. Формулы Литтла

Задания на лабораторную работу

1. Задать матрицу вероятностей перехода
2. Проверить непротиворечивость
3. Найти финальные вероятности по формуле Эрланга
4. Вывести траектории при разных начальных условиях и проверить их соответствие формулам Эрланга
5. Задать матрицу интенсивностей вероятностей перехода, смоделировать СМО, вывести траектории, проверить их соответствие формулам Эрланга