Основные свойства простейшего потока

  Рассмотрим семейство случайных величин y (τ) = x (t, t +τ) = x (0, τ) - число вызовов на интервале длины τ – его распределение не зависит от t.  

Утв. y (τ) – марковская цепь с непрерывным временем.

  Действительно, для любых

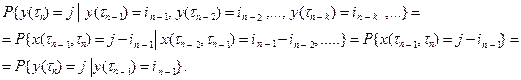
Найдем ее инфинитезимальную матрицу (матрицу интенсивностей вероятностей перехода):

Таким образом, получается матрица бесконечной размерности

.

Решим для нее систему уравнений Колмогорова :

.

  Утв. 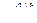= - k -я диагональ состоит из единиц, остальные нули.

Таким образом, получилось, что y (τ) подчиняется закону Пуассона с параметром :

.

Следствие.

Финальных вероятностей в обычном смысле у цепи y (τ) не существует, с вероятностью 1 процесс уходит на бесконечность, но при действует нормальная аппроксимация

  Пусть T – случайная величина, равная времени ожидания очередного вызова в простейшем потоке с интенсивностью λ. Ее функция распределения  - вероятность того, что на промежутке длиной t не появилось ни одного вызова, так что

Таким образом, величина T подчиняется экспоненциальному закону с параметром λ:

       Утв.

       Пусть  Тогда

то есть распределение времени ожидания очередного вызова не зависит от наличия информации о том, что вызовов уже не было в течение промежутка длиной τ. Это – другая формулировка свойства отсутствия последействия.

  Аналогично, если поток х является стационарным и  то

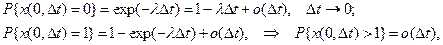
так что такой поток автоматически оказывается простейшим.

Следствие. Моделью простейшего потока является вариационный ряд, построенный по выборке n случайных точек из равномерного распределения U (0, a) при больших n, a. Среднее расстояние между такими точками, очевидно, равно a / n, оно равно среднему значению времени ожидания MT, откуда интенсивность потока λ= = n / a.

Важно:

Показательный закон – единственный закон распределения времени ожидания вызова, для которого информация о том, сколько времени продолжалось ожидание, не влияет на закон распределения оставшегося времени.