Оценивание коэффициентов параметрических моделей

Коэффициенты { a_i }, i =1,…, p в в модели AR (p)

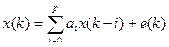
можно оценить по МНК на основе простейшей линейной модели, хотя эта оценка и не является оптимальной. Действительно, пусть наблюдается отрезок временного ряда – вектор Y = [ x (p +1), x (p +2),…, x (n)] ^T. Введем вектор коэффициентов и составим матрицу

Тогда оценка вектора a по МНК имеет вид и из неё легко получить оценку дисперсии порождающего шума :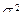

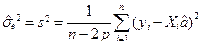где X_i – i -я строка матрицы X. Потеря точности здесь связана с тем, что компоненты матрицы X являются случайными величинами, а компоненты Y коррелированны.

Другая возможность - получить оценки ковариаций K (0), K (1),…. и оценить коэффициенты модели из уравнений Юла-Уокера. Здесь основная сложность состоит в получении несмещенных оценок ковариаций и в определении их правильного числа. Обычно их берут больше, чем порядок модели p, и решают систему уравнений Юла-Уокера по МНК. Более сложный способ состоит в том, чтобы получить непараметрическую оценку спектральной плотности S (f) и аппроксимировать ее в классе спектральных плотностей процессов AR (p) – на этом пути оценка оказывается линейной.

Для моделей, содержащих часть в виде скользящего среднего, чаще всего используют уравнения Юла-Уокера или одну из гибридных схем. Например, исходный ряд можно аппроксимировать моделью авторегрессии завышенного порядка, а затем, оперируя полиномами от оператора сдвига 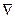, получить модель с меньшим числом параметров. Для этого имеется специфическая техника – аппроксимации Паде. Рассмотрим один из наиболее практичных субоптимальных алгоритмов - оценивание параметров ARMA -модели в замкнутом контуре.

Модель ARMA (p, q) может быть записана в виде

x (k) = c^Tz (k) + e (k), (9.4)

где

z (k) = [ x (k -1),…., x (k-p), e (k -1),…., e (k-q) ] ^T, c = [ a ₁,…, a_p, b ₁,…, b_q ] ^T.

Формально представление (15) эквивалентно AR -представлению и для оценивания вектора коэффициентов с можно использовать МНК в обычной или рекуррентной форме. Однако здесь величины { e (k)} ненаблюдаемы. Одно из преимуществ МНК в рекуррентной форме состоит в том, что для очередного шага можно использовать оценки , полученные на предыдущих шагах: