Движение независимых заряженных частиц в электромагнитных полях

Лекция ДО_2

Обращаю ваше внимание, что перед рассмотрением более общей задачи в настоящей лекции вам необходимо отдельно тщательно проанализировать движение ионов и электронов в простейших электромагнитных конфигурациях (см. заключительную часть 1-й лекции в рамках ДО – ДО_1), когда частицы движутся в стационарном и однородном только либо электрическом, либо магнитном поле.

Такой анализ должен включать: а) определение направления ускорения частиц различных зарядов в электрическом поле или их вращения в магнитном поле; б) оценки характерных частот и периодов вращения электронов и ионов вокруг магнитных силовых линий (МСЛ) и их сравнение (например, для индукций 0,01, 0,1 и 1 Тл), в) оценки циклотронных радиусов вращения различных частиц вокруг МСЛ (например, для индукций 0,01, 0,1 и 1 Тл и тепловых скоростей частиц, соответствующих температурам 1, 10 эВ и 1, 5, 10, 20, 50 кэВ).

 

       При движении только в магнитном поле изменяется лишь перпендикулярная вектору индукции проекция скорости, поэтому часто говорят, что уравнение движения описывает лишь поперечную составляющую скорости частицы. Нетрудно показать, что в этом случае кинетическая энергия частицы должна сохраняться. Для этого достаточно обе части записанного ранее в отсутствие других сил, кроме силы Лоренца (оно носит также название уравнения Ньютона – Лоренца), уравнения движения

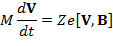
скалярно умножить на вектор скорости 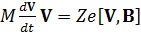V:

  V.

Правая часть этого уравнения обращается в нуль, поскольку результат векторного произведения перпендикулярен вектору скорости, а левую часть можно представить в следующем виде:

 .

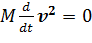Но это и есть производная по времени от кинетической энергии частицы. Таким образом, закон сохранения кинетической энергии можно записать так:

 

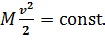
Продолжим анализ движения частиц в рамках введенного в предыдущей лекции дрейфового приближения. Напомню, что в этом приближении, которое было предложено великим физиком Энрико Ферми, выделяют три составляющие скорости: а) быстрое вращение частиц по окружности вокруг магнитной силовой линии (этот вид движения частиц в однородном стационарном магнитном поле при отсутствии электрического поля и каких-либо других сил, действующих на частицу, был рассмотрен в конце предыдущей лекции), б) дрейфовое движение центра ларморовской окружности (так называемого ведущего центра) перпендикулярно вектору магнитной индукции В, в). «почти свободное» движение частиц в направлении, коллинеарном вектору B. Термин в кавычках (в отличие от часто применяемого «свободное движение частиц вдоль В») будет проанализирован далее при описании движения частиц в сложных магнитных конфигурациях. Обратим внимание, что жирным прямым шрифтом мы обозначаем вектор какой-то величины (например, силы F, скорости V, ускорения a) или его проекцию, перпендикулярную или коллинеарную вектору B (например, F _^, V _^, F _ǁ, V _ǁ), а наклонным – модуль вектора (например, v) или проекции вектора на выделенное направление (например, v _^, v _ǁ).

Итак, используем уравнение движения отдельной заряженной частицы с массой M и зарядом Ze в следующем виде:

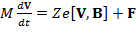,                                    (1)

где F – равнодействующая всех (кроме силы Лоренца) сил, действующих на частицу (электростатической, гравитационной, силы взаимодействия с другими частицами и т.д.). Взаимодействием частиц в рассматриваемом приближении пренебрегаем. Кроме того, рассмотрим случай, когда сила F имеет только проекцию, перпендикулярную вектору В. В ее присутствии возникает дрейфовое движение.

       Природа дрейфового движения.

Рассмотрим проекцию траектории заряженной частицы на плоскость, перпендикулярную вектору магнитной индукции (рис. 1).

Пусть вектор магнитной индукции (постоянный во времени и в пространстве) направлен на нас, а вращение частицы происходит по часовой стрелке (определите, как заряжена эта частица!!!). Поскольку сила F направлена вправо, при движении по верхней половине окружности частица ускоряется, а по нижней – замедляется.

В результате модуль скорости в точке А будет меньше модуля скорости в точке В:

| V _B | > | V _А |,

что должно привести к смещению траектории частицы вниз.

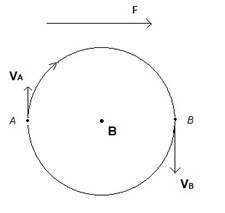
Рис. 1

       Простая оценка разности скоростей в этих точках может быть получена из уравнения движения. Т.к. в соответствии со вторым законом Ньютона ускорение a пропорционально действующей силе (обозначим ее через F _^) a = F _^ / M, то умножив его значение на характерное время, обратно пропорциональное циклотронной частоте вращения частицы ω _с, получим приближенную оценку ∆ v:

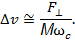
       Для получения формулы для скорости смещения циклотронной окружности вспомним, что в дрейфовом приближении выделяют 2 составляющих скорости, перпендикулярные вектору В. Рассмотрим эти составляющие более подробно:

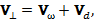                                                     (2)

где первое слагаемое представляет собой скорость вращения частицы вокруг магнитной силовой линии, а второе означает скорость смещения ведущего центра ларморовской окружности перпендикулярно вектору магнитной индукции.

       Подставляя выражение (2) в уравнение движения (1) для поперечной (т.е. перпендикулярной вектору индукции) составляющей скорости

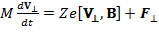                                                ,                                             (3)

получим:

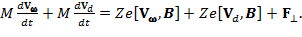                          (4)

       Обратим внимание, что в предыдущей лекции мы получали выражение для скорости вращения частицы вокруг магнитной силовой линии (мы обозначили сейчас эту скорость через 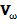), используя уравнение движения Ньютона – Лоренца в виде (3), но только в отсутствие внешней силы F _^. Поэтому первые слагаемые в левой и правой частях уравнения (4) тождественно равны друг другу, т.е.

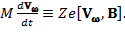                                               (5)

       Тогда, сокращая в выражении (4) равные друг другу первые слагаемые в левой и правой его частях, получим уравнение для нахождения скорости дрейфа :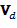

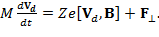                                      (6)

       Решим уравнение (6), предполагая, что искомая величина 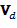 не зависит от времени, т.е. пренебрегая производной от скорости дрейфа от времени (на правомерности этого предположения мы остановимся несколько позже):

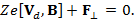                                           (7)

Скорость 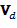 заключена в последнем уравнении внутри векторного произведения. Для ее определения используем известный в векторной алгебре прием: умножим уравнение (7) векторно справа на В:

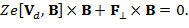                                          (8)

Перенося второе слагаемое в правую часть и изменяя порядок векторных сомножителей, получим:

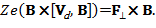                                             (9)

       Раскрывая в левой части уравнения (9) тройное векторное произведение по правилу

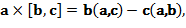
т.е.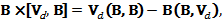                                  

и учитывая перпендикулярность скорости дрейфа вектору магнитной индукции (в результате чего последнее слагаемое в правой части последнего уравнения обращается в нуль), получим следующее выражение для скорости дрейфа:

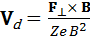     .                                                    (10)

       Напомню, что эта скорость приписывается не самой частице, а центру циклотронной окружности, а ее величина должна быть значительно меньше скорости вращения частицы 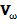. Кроме того, необходимо подчеркнуть, что в соответствии с определением векторного произведения вектор скорости  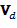перпендикулярен как вектору действующей силы, так и вектору магнитной индукции.

       Обратим внимание, что в уравнении (10) величине действующей силы пропорционально значение скорости дрейфа, а не ускорения, как это следовало бы из второго закона Ньютона! В чем тут дело (не работает какой-то из упомянутых законов либо при выводе сделано какое-то некорректное допущение и т.д.?) – предполагаю порассуждать каждому самостоятельно, а потом при встрече мы коллективно обсудим этот парадокс….