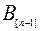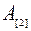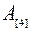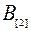Прежде, чем переходить к рассмотрению общих случаев построения расписаний обработки, рассмотрим более простой класс задач, когда все детали обрабатываются на станках в одной и той же последовательности. Такие системы, как уже отмечалось в предыдущих лекциях, называют конвейерными системами.
Расписания работ для конвейерных систем строятся гораздо легче, чем для систем произвольной структуры. Однако простота построения расписаний для таких систем относительна и для них существует еще много нерешенных задач.
Для конвейерных систем получены весьма интересные результаты, которые значительно упрощают построение расписания обработки.
Рассмотрим более подробно такие результаты, которые формулируются в следующих двух теоремах.
Теорема 2.4.1. Если составляется расписание обработки 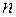 деталей в конвейерной системе из
деталей в конвейерной системе из 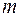 машин и все детали доступны одновременно, то оптимальное, с точки зрения минимума времени обработки всех деталей, расписание принадлежит классу расписаний, в которых одинаков порядок выполнения работ на двух первых машинах.
машин и все детали доступны одновременно, то оптимальное, с точки зрения минимума времени обработки всех деталей, расписание принадлежит классу расписаний, в которых одинаков порядок выполнения работ на двух первых машинах.
Доказательство. Когда в расписании порядок выполнения работ на первых двух машинах различен, то всегда можно найти такую пару работ 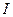 и
и 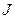 , что на первой машине
, что на первой машине 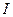 непосредственно предшествует
непосредственно предшествует 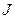 , а на второй машине
, а на второй машине 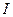 следует за
следует за 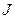 . При этом в общем случае между работами
. При этом в общем случае между работами 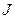 и
и 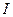 на втором станке возможны какие-либо промежуточные работы. Такая ситуация может быть представлена на следующем рисунке (Рис. 10.19).
на втором станке возможны какие-либо промежуточные работы. Такая ситуация может быть представлена на следующем рисунке (Рис. 10.19).
| Машина 1 | … | I | J | … | ||||
| Машина 2 | … | J | … | I | … | |||
Рис. 10.19. Различная последовательность работ 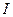 и
и 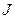 на первой и второй машинах.
на первой и второй машинах.
Понятно, что последовательность работ 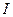 и
и 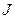 на первой машине можно изменить на обратный, не вызывая при этом никакого дополнительного сдвига в начале выполнения любой из этих работ на второй машине и, следовательно, всех последующих. Такая перестановка не может привести к возрастанию времени окончания всех последующих работ и, следовательно, не увеличит времени выполнения всех работ. Однако с другой стороны может случиться, что в результате подобной перестановки начала некоторых работ можно будет сместить влево и сократить время выполнения всех работ. Невозможность возрастания времени окончания всех работ при такой перестановке уже доказывает данную теорему.
на первой машине можно изменить на обратный, не вызывая при этом никакого дополнительного сдвига в начале выполнения любой из этих работ на второй машине и, следовательно, всех последующих. Такая перестановка не может привести к возрастанию времени окончания всех последующих работ и, следовательно, не увеличит времени выполнения всех работ. Однако с другой стороны может случиться, что в результате подобной перестановки начала некоторых работ можно будет сместить влево и сократить время выполнения всех работ. Невозможность возрастания времени окончания всех работ при такой перестановке уже доказывает данную теорему.
Теорема 2.4.2. Если составляется расписание обработки 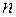 деталей в конвейерной системе из
деталей в конвейерной системе из 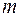 машин и все детали доступны одновременно, то оптимальное, с точки зрения минимума времени обработки всех деталей, расписание принадлежит классу расписаний, в которых одинаков порядок выполнения работ на двух первых (1 и 2) и двух последних (
машин и все детали доступны одновременно, то оптимальное, с точки зрения минимума времени обработки всех деталей, расписание принадлежит классу расписаний, в которых одинаков порядок выполнения работ на двух первых (1 и 2) и двух последних (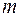 -1 и
-1 и 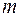 ) машинах.
) машинах.
Доказательство. Первая часть теоремы, касающаяся одинакового порядка обработки двумя первыми машинами, следует из первой теоремы.
Предположим теперь, что порядок выполнения работ на двух последних машинах различен. Тогда можно найти пару работ 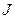 и
и 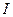 на
на 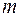 -ой машине, что работа
-ой машине, что работа 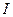 на
на 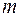 -ой машине непосредственно следует за работой
-ой машине непосредственно следует за работой 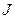 , а на (
, а на (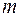 -1)-ой машине порядок следования этих работ является обратным. Причем между работами
-1)-ой машине порядок следования этих работ является обратным. Причем между работами 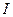 и
и 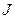 на (
на (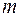 -1)-й машине возможны другие промежуточные работы. Такая ситуация может быть представлена на следующем рисунке (Рис. 10.20).
-1)-й машине возможны другие промежуточные работы. Такая ситуация может быть представлена на следующем рисунке (Рис. 10.20).
| Машина m -1 | … | I | … | J | … | |||
| Машина m | … | J | I | … | ||||
Рис. 10.20. Различная последовательность работ 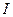 и
и 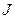 на (
на (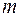 -1)-ой и
-1)-ой и 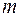 -ой машинах.
-ой машинах.
Из данного рисунка видно, что порядок выполнения работ на 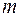 -ой машине можно изменить на обратный, не увеличивая длительности прохождения этих работ и не изменяя длительности прохождения последующих работ на
-ой машине можно изменить на обратный, не увеличивая длительности прохождения этих работ и не изменяя длительности прохождения последующих работ на 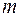 -ой машине. Однако возможна ситуация, когда в результате такой перестановки начала некоторых работ на
-ой машине. Однако возможна ситуация, когда в результате такой перестановки начала некоторых работ на 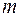 -й машине можно будет сместить влево и сократить время выполнения всех работ, что уже и доказывает данную теорему.
-й машине можно будет сместить влево и сократить время выполнения всех работ, что уже и доказывает данную теорему.
Таким образом, из этих теорем получаем, что для определения оптимального с точки зрения времени обработки для конвейерной системы из двух машин достаточно рассматривать только такие расписания, когда детали на второй машине обрабатываются в таком же порядке, что и на первой машине.
Для конвейерной системы из трех машин также достаточно для получения оптимального с точки зрения времени обработки рассматривать только такие расписания, в которых детали на второй и третьей машинах обрабатываются в таком же порядке, что и на первой машине.
Однако уже для конвейерной системы из четырех машин оптимальные расписания с точки зрения минимизации времени обработки могут не принадлежать классу расписаний, в которых порядок обработки деталей на всех машинах одинаковый.
В качестве примера рассмотрим задачу построения оптимального, с точки зрения минимизации времени обработки, расписания для конвейерной системы из четырех машин, на которой обрабатываются две детали. Исходные данные для такой задачи представлены в табл. 10.5.
Таблица 10.5
| Длительности обработки в часах | ||||
| Станок | I | II | III | IV |
| Деталь I | 4 | 1 | 1 | 4 |
| Деталь J | 1 | 4 | 4 | 1 |
Существуют только два расписания с одинаковым порядком выполнения работ на каждой машине (рис.10.21, рис.10.22).
| Машина 1 | I | J |
| ||||
| Машина 2 | I | J |
| ||||
| Машина 3 |
| I | J | ||||
| Машина 4 |
| I | J | ||||
Рис. 10.21. Порядок выполнения работ I-J (длительность 14 час).
| Машина 1 | J | I |
|
| ||
| Машина 2 | J | I |
| |||
| Машина 3 | J | I | ||||
| Машина 4 |
| J | I | |||
Рис. 10.22. Порядок выполнения работ J-I (длительность 14 час).
Максимальная длительность прохождения работ в этих случаях будет равна 14 часам. Теперь рассмотрим расписание с одинаковым порядком J-I на первых двух машинах и обратным порядком выполнения работ на машинах 3 и 4. Такое расписание представлено на рис.10.23.
| Машина 1 | J | I |
| |||
| Машина 2 | J | I |
| |||
| Машина 3 | I | J | ||||
| Машина 4 | I | J | ||||
Рис. 10.23. Порядок выполнения работ J-I на первых двух машинах и I-J на двух последних (длительность 12 час).
Максимальная длительность прохождения работ в этом случае равна 12 часам, т. е. меньше, чем в расписаниях с одинаковым порядком выполнения работ на всех машинах.
Такая же картина сохраняется и для большего количества машин при конвейерной обработке деталей.
Перейдем теперь к более подробному рассмотрению одной из важнейших задач теории расписаний, которая оказала огромное влияние на все последующие работы в этой области, к задаче Джонсона.
Задача Джонсона формулируется следующим образом. Пусть имеется два станка, на которых требуется обработать 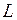 деталей. Каждая деталь обрабатывается сначала на первом станке, а потом – на втором. Известны времена обработки каждой детали на каждом станке. Имеются также ограничения, которые состоят в следующем:
деталей. Каждая деталь обрабатывается сначала на первом станке, а потом – на втором. Известны времена обработки каждой детали на каждом станке. Имеются также ограничения, которые состоят в следующем:
1. На одном станке одновременно не может обрабатываться больше одной детали.
2. Одна деталь одновременно не может обрабатываться на нескольких станках. Причем обработка любой детали на первом станке должна завершиться раньше, чем начнется ее обработка на втором станке.
В задаче требуется таким образом определить порядок запуска деталей на обработку, чтобы общее время обработки всех 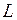 деталей оказалось бы минимальным.
деталей оказалось бы минимальным.
Большая заслуга Джонсона оказалась не только в том, что он обратил внимание на разную длительность обработки деталей на станках в зависимости от их порядка обработки, но и предложил алгоритм построения оптимального по времени расписания обработки деталей на двух станках при указанных выше предположениях.
К сожалению, задача Джонсона оказалась одной из двух задач в теории расписаний, для которой может быть построен алгоритм формирования оптимальных расписаний. Для других задач, особенно для задач имеющих прикладное значение пока таких алгоритмов построить не удается.
Для изложения алгоритма Джонсона и доказательства его оптимальности удобно принять предложенные Джонсоном обозначения.
Пусть через 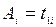 обозначено время обработки
обозначено время обработки 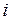 -ой детали на первом станке, через
-ой детали на первом станке, через 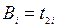 − время обработки
− время обработки 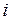 -ой детали на втором станке, а через
-ой детали на втором станке, а через 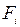 − длительность прохождения обработки
− длительность прохождения обработки 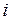 -ой деталью, т. е. время окончания обработки
-ой деталью, т. е. время окончания обработки 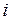 -ой детали на втором станке.
-ой детали на втором станке.
Таким образом, каждая обработка 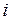 -ой детали характеризуется парой (
-ой детали характеризуется парой (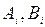 ), где
), где 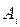 − время обработки на первом станке, а
− время обработки на первом станке, а 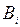 − на втором. Такое разбиение существует для всех деталей, хотя некоторые из значений
− на втором. Такое разбиение существует для всех деталей, хотя некоторые из значений 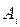 или
или 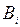 могут быть равными нулю, т. е. некоторые детали могут не обрабатываться либо на первом, либо на втором станке.
могут быть равными нулю, т. е. некоторые детали могут не обрабатываться либо на первом, либо на втором станке.
Из приведенных выше теорем следует, что нужно рассматривать только расписания с одинаковым порядком выполнения работ каждым станком.
В последующем изложении целесообразно использовать обозначения, где индекс в квадратных скобках означает очередность обработки деталей, например, через  обозначено время, затрачиваемое первым станком на обработку второй детали в очереди. Расписание может быть представлено как на рис.10.24.
обозначено время, затрачиваемое первым станком на обработку второй детали в очереди. Расписание может быть представлено как на рис.10.24.
| Станок 1 | 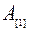 |  |
| 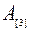 | … | 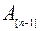 |
| |||||
| Станок 2 |
|
| … |
|  | |||||||
Рис. 10.24. Расписание выполнения работ в задаче Джонсона.
Поскольку  не перекрывается с
не перекрывается с  , то обработка последней детали на втором станке не может быть окончена до завершения обработки всех деталей на первом станке и окончания обработки последней детали на втором станке. Поэтому
, то обработка последней детали на втором станке не может быть окончена до завершения обработки всех деталей на первом станке и окончания обработки последней детали на втором станке. Поэтому
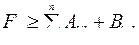 ,
,
где 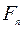 - длительность обработки
- длительность обработки 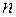 деталей на двух станках. С другой стороны, окончание обработки деталей не может окончиться до завершения обработки деталей на втором станке и, учитывая, что обработка первой детали на втором станке не может начаться раньше, чем через интервал времени
деталей на двух станках. С другой стороны, окончание обработки деталей не может окончиться до завершения обработки деталей на втором станке и, учитывая, что обработка первой детали на втором станке не может начаться раньше, чем через интервал времени 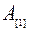 , получаем
, получаем
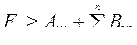 .
.
Отметим, что 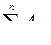 и
и 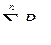 не зависят от последовательности обработки деталей и определяются исходными данными. Поэтому уменьшить приведенные нижние границы можно лишь за счет
не зависят от последовательности обработки деталей и определяются исходными данными. Поэтому уменьшить приведенные нижние границы можно лишь за счет 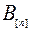 и
и 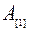 с помощью соответствующего упорядочения. Для этого нужно выбрать работы с наименьшими
с помощью соответствующего упорядочения. Для этого нужно выбрать работы с наименьшими 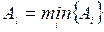 (
(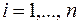 )и
)и 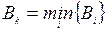 (
(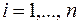 ). Работу с наименьшим значением времени обработки на первом станке
). Работу с наименьшим значением времени обработки на первом станке 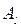 целесообразно выполнять первой и тогда
целесообразно выполнять первой и тогда 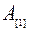 будет минимальной, а работу с наименьшим значением времени обработки на втором станке
будет минимальной, а работу с наименьшим значением времени обработки на втором станке 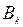 целесообразно выполнять последней и
целесообразно выполнять последней и 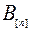 будет минимальной.
будет минимальной.
После того как размещены две работы, можно применить те же самые рассуждения к оставшимся (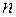 -2) работам.
-2) работам.
Следует заметить, что приведенные рассуждения не являются строгими и поэтому нельзя быть уверенным, что описанное упорядочение всегда будет приводить к хорошим результатам. Не ясно также, что произойдет на последнем шаге рекуррентной процедуры, однако в инженерной практике этот метод получил широкое распространение.
В основе алгоритма, предложенного Джонсоном, лежат неравенства, похожие на приведенные выше. Однако Джонсону удалось доказать оптимальность своего алгоритма.
Очевидно, что можно ограничиться рассмотрением расписаний, в которых работы на первом станке «упакованы» плотно, начиная с первой из них, т. е. первый станок работает без простоев до завершения обработки 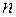 -ой детали.Понятно, что к подобному расписанию может быть приведено любое произвольное расписание путем соответствующих сдвигов влево всех назначений в нем, пока не будет достигнута нужная плотность. Очевидно, что эта процедура не приведет к возрастанию максимальной длительности прохождения.
-ой детали.Понятно, что к подобному расписанию может быть приведено любое произвольное расписание путем соответствующих сдвигов влево всех назначений в нем, пока не будет достигнута нужная плотность. Очевидно, что эта процедура не приведет к возрастанию максимальной длительности прохождения.
Пусть 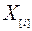 - время простоя второй машины, непосредственно предшествующее
- время простоя второй машины, непосредственно предшествующее 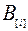 . Типичное расписание имеет вид как на рис.10.25.
. Типичное расписание имеет вид как на рис.10.25.
| Станок 1 | 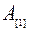 |
| 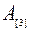 |
| … | 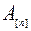 |
| ||||
| Станок 2 |  | 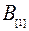 |  |
| 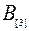 |  | … | 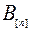 | |||
Рис. 10.25. Расписание выполнения работ
Значения 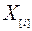 могут быть выражены через
могут быть выражены через 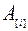 и
и 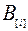 следующим образом:
следующим образом:
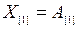 ,
, 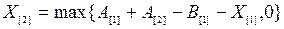 ,
,
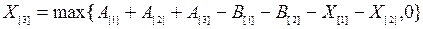
В общем случае можно написать
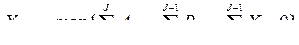 .
.
Определим частные суммы
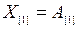 ,
, 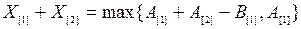

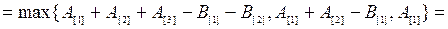
 .
.
Вообще,
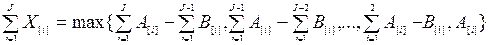
Если определить 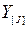 как
как
 то
то
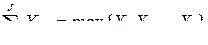 .
.
Если обозначить через 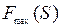 длительность обработки
длительность обработки 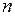 деталей для конкретного расписания
деталей для конкретного расписания 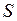 , то, как видно из приведенной выше диаграммы Гантта, величина
, то, как видно из приведенной выше диаграммы Гантта, величина 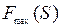 будет равна:
будет равна:
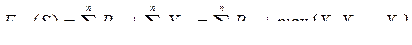 .
.
Поскольку 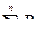 не зависит от расписания, минимальная длительность расписания зависит только от суммы интервалов простоя второго станка, что эквивалентно минимизации следующей величины:
не зависит от расписания, минимальная длительность расписания зависит только от суммы интервалов простоя второго станка, что эквивалентно минимизации следующей величины:
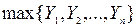 .
.
Поэтому задача отыскания оптимального расписания 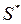 такого, что
такого, что 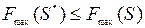 для любого
для любого 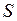 сводится к минимизации
сводится к минимизации 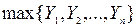 .
.
Алгоритм решения данной задачи, который был предложен Джонсоном, сформулирован в следующей теореме [11-12].
Теорема Джонсона.
В конвейерной системе из двух машин при обработке L деталей и одновременной доступности всех работ, упорядочение, которое минимизирует максимальную длительность прохождения таково, что работа j предшествует работе j+1, если 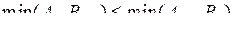 и
и 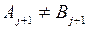 .
.
Если 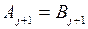 и существует ряд следующих за ней работ
и существует ряд следующих за ней работ 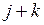
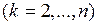 , для которых также
, для которых также 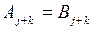 , то для этих работ кроме выполнений условий
, то для этих работ кроме выполнений условий 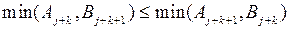
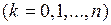 , должно выполняться соотношение
, должно выполняться соотношение 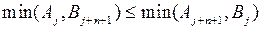 , где через
, где через 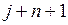 обозначена первая работа, следующая за работами
обозначена первая работа, следующая за работами 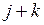
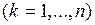 и для которой
и для которой 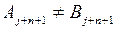 .
.
Доказательство.
В соответствии с неравенством, содержащимся в утверждении теоремы, работа j помещается на место J, а работа 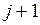 помещается на место
помещается на место 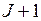 если
если
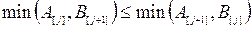 или
или
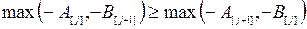 или
или
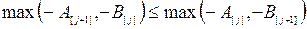 (10.21)
(10.21)
Рассмотрим теперь величину
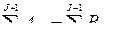 (10.22).
(10.22).
Эта величина не зависит от порядка выполнения работ. Прибавим (2) к левой части (1).
Если 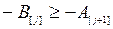 , то
, то 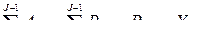 .
.
Если 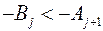 , то
, то 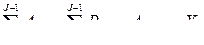 при размещении работы j на месте J.
при размещении работы j на месте J.
Прибавим (10.22) к правой части (10.21), получим:
если 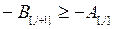 , то
, то  ,
,
если 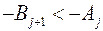 , то
, то 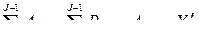
при размещении работы j+1 на 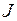 -м месте.
-м месте.
Если размещение работ выполняется в соответствии с неравенством, содержащимся в утверждении теоремы, то
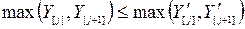 (10.23).
(10.23).
Это неравенство следует из неравенства (10.21), так как ко всем его частям прибавляется одна и та же величина.
Из неравенства (10.23) следует, что при размещении работ j и j+1 на места 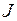 и
и 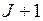 максимум простоев оборудования будет не выше, чем при обратном расположении.
максимум простоев оборудования будет не выше, чем при обратном расположении.
Поскольку ни одно из других значений 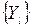 не изменяется в результате размещения работ j и j+1 на места
не изменяется в результате размещения работ j и j+1 на места 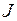 и
и 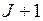 , то максимум
, то максимум 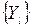 или не изменится, или уменьшится в результате указанной расстановки.
или не изменится, или уменьшится в результате указанной расстановки.
Транзитивность соотношений
Для доказательства теоремы нам нужно так же показать, что для работ i, j и k, если
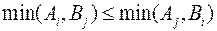 (10.24)
(10.24)
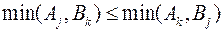 , (10.25)
, (10.25)
то должно выполняться
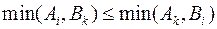 .
.
Это необходимо, так как если работа i предшествует работе j, а работа j предшествует работе k, то работа i должна предшествовать и работе k. Иначе формулировка теоремы будет противоречивой.
Случай 1.
Пусть 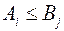 и
и  , тогда из (10.24) и (10.25) имеем
, тогда из (10.24) и (10.25) имеем
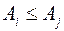 и
и 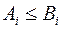 , а
, а
 и
и  .
.
Отсюда получаем, что 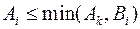 и поэтому какова бы ни была величина
и поэтому какова бы ни была величина 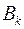
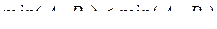 .
.
Случай 2.
Пусть 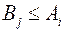 ,
,  тогда из (10.24) и (10.25) имеем
тогда из (10.24) и (10.25) имеем
 и
и 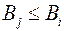 , а
, а
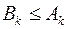 и
и 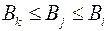 .
.
Отсюда получаем, что 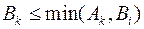 и поэтому какова бы ни была величина
и поэтому какова бы ни была величина 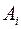
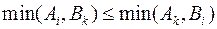 .
.
Случай 3.
Пусть 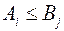 и
и  тогда из (10.24) и (10.25) имеем
тогда из (10.24) и (10.25) имеем
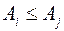 и
и 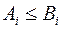 , а
, а
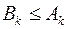 и
и 
Отсюда получаем, что 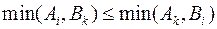 , так как если
, так как если 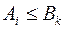 , то
, то 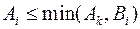 поскольку
поскольку 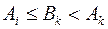 и
и 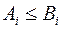 .
.
Если же 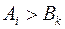 , то
, то 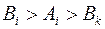 и
и 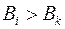 , и
, и 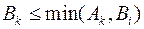 .
.
Случай 4.
Пусть 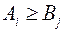 и
и  тогда из (10.24) и (10.25) имеем
тогда из (10.24) и (10.25) имеем
 и
и 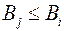 , а
, а
 и
и 
Отсюда получаем, что  и
и  , то есть
, то есть 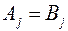 . В случае равенства
. В случае равенства 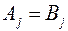 и следующих за ней работ
и следующих за ней работ 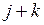 (
(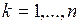 ), для которых также выполняются равенства
), для которых также выполняются равенства 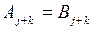 , в соответствии с условиями теоремы кроме выполнения неравенств
, в соответствии с условиями теоремы кроме выполнения неравенств 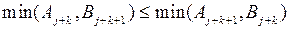
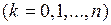 , требуется выполнение соотношений
, требуется выполнение соотношений 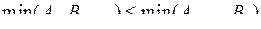 , где через
, где через 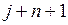 обозначена первая работа, следующая за работами
обозначена первая работа, следующая за работами 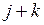
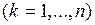 , для которой
, для которой 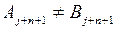 . Это обеспечивает выполнение условий транзитивности в этом случае. Теорема доказана.
. Это обеспечивает выполнение условий транзитивности в этом случае. Теорема доказана.
Необходимость выполнения неравенств 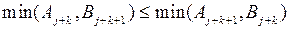
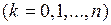 и
и 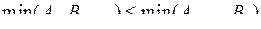 обусловлена тем, что без выполнения этих условий возможна ситуация, когда условия
обусловлена тем, что без выполнения этих условий возможна ситуация, когда условия
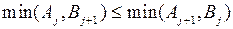
выполняются для всех 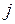 , а расписание не будет оптимальным.
, а расписание не будет оптимальным.
Действительно, рассмотрим следующую задачу Джонсона.
Пусть имеется два станка, на которых требуется обработать 3 детали. Каждая деталь обрабатывается сначала на первом станке, а потом – на втором. Времена обработки каждой детали на каждом станке заданы в следующей таблице.
Таблица 10.7
| Первый станок | Второй станок | |
| Первая деталь | 30 | 5 |
| Вторая деталь | 4 | 4 |
| Третья деталь | 5 | 30 |
Рассмотрим две последовательности запуска деталей на обработку:
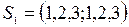 и
и 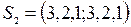 .
.
В первой последовательности на первом станке сначала обрабатывается первая деталь, затем вторая и, наконец, третья. На втором станке детали обрабатываются в таком же порядке. Рассмотрим выполнение условий
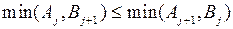
для такого порядка обработки деталей:
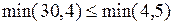 ,
, 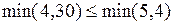 .
.
Как видно из этих соотношений, условия Джонсона для такой последовательности обработки выполняются, а диаграмма Гантта для нее будет иметь вид, представленный на рис. 10.26.

Рис. 10.26. Диаграмма Гантта для обработки деталей в последовательности 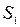 .
.
В другой последовательности на первом станке сначала обрабатывается третья деталь, затем вторая и, наконец, первая. На втором станке детали обрабатываются в таком же порядке. Проверим выполнение условий
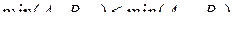
для такого порядка обработки деталей:
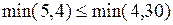 ,
, 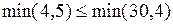 .
.
Как видно из этих соотношений, условия Джонсона для такой последовательности обработки также выполняются, и диаграмма Гантта для такой последовательности обработки деталей будет иметь вид, представленный на рис. 10.27.

Рис. 10.27. Диаграмма Гантта для обработки деталей в последовательности 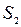 .
.
Как следует из этих диаграмм Гантта время завершения работ, которые выполняются в последовательности 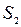 , будет существенно меньше, чем время выполнения работ в последовательности
, будет существенно меньше, чем время выполнения работ в последовательности 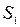 , хотя условия
, хотя условия
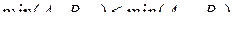
выполняются как для последовательности 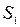 , так и для последовательности
, так и для последовательности 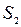 .
.
Поэтому выполнение неравенств
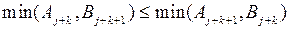
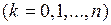
и
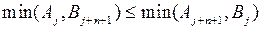
позволит избежать таких ситуаций.
Еще одной задачей, для решения которой может быть построен алгоритм, позволяющий получать оптимальное решение, является задача, в которой требуется на двух машинах выполнить ряд работ при условии, что часть работ выполняется сначала на одной машине, затем – на другой, а другая часть работ выполняется в обратном порядке.
Джексон показал, что эта задача есть небольшое обобщение конвейерной задачи с двумя машинами, рассмотренной Джонсоном, и что для решения требуется лишь небольшая модификация алгоритма Джонсона. Это значит, что задача с произвольным числом работ требует сравнительно небольшого объема вычислений.
Решение начинается с разбиения п работ на четыре подмножества следующим образом:
{ А }— подмножество работ, состоящих из единственной операции, выполняемой на машине 1;
{ В }— подмножество работ, состоящих из единственной операции, выполняемой на машине 2;
{ АВ } — подмножество работ, состоящих из двух операций, из которых первая выполняется машиной 1, а вторая — машиной 2;
{ ВА }— подмножество работ, состоящих из двух операций, из которых первая выполняется машиной 2, а вторая — машиной 1.
После этого работы из подмножества { АВ }упорядочиваются в соответствии с алгоритмом Джонсона независимо от остальных работ, и то же проделывается с работами из { ВА }. Упорядочение работ из множеств { А } и { В }не влияет на максимальную длительность прохождения и может быть произвольным. Джексон показал, что оптимальным является следующий порядок выполнения работ;
а) машина 1 выполняет работы из { АВ }, упорядоченные в соответствии с условиями оптимальности Джонсона, после этого работы из множества { А }, и, наконец, из множества { ВА };
б) машина 2 выполняет работы из множества { ВА }, упорядоченные в соответствии с условиями оптимальности Джонсона,затем из { В }, и, наконец, из множества { АВ }, причем порядок выполнения внутри каждого из подмножеств сохраняется.
Легко видеть, что такое расписание оптимально. Действительно, так как длительности выполнения операций фиксированы, то качество расписания определяется фактически длиной свободных интервалов (длительностей простоя) между выполнением отдельных операций. Если 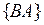 пусто, то очевидно, что для работ из { А }, { В }и { АВ }расписание является оптимальным. При этом длительность простоя машины 2 будет минимальной. Рассмотрим теперь работы из { ВА }. Они могут быть выполнены на машине 2 без простоев между операциями, выполнение же их на машине 2 прежде остальных работ приведет к возможной задержке выполнения работ из { АВ }на этой машине. Последнее обстоятельство может лишь уменьшить простои между выполнением операций работ подмножества { АВ }на машине 2. Очевидно, нет смысла рассматривать расписания, в которых работы из { АВ }выполняются машиной 2 до окончания всех работ из
пусто, то очевидно, что для работ из { А }, { В }и { АВ }расписание является оптимальным. При этом длительность простоя машины 2 будет минимальной. Рассмотрим теперь работы из { ВА }. Они могут быть выполнены на машине 2 без простоев между операциями, выполнение же их на машине 2 прежде остальных работ приведет к возможной задержке выполнения работ из { АВ }на этой машине. Последнее обстоятельство может лишь уменьшить простои между выполнением операций работ подмножества { АВ }на машине 2. Очевидно, нет смысла рассматривать расписания, в которых работы из { АВ }выполняются машиной 2 до окончания всех работ из 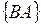 и { В }. Действительно, допустим, что мы попытаемся выполнить работу К из { ВА }на машине 2 во время простоя
и { В }. Действительно, допустим, что мы попытаемся выполнить работу К из { ВА }на машине 2 во время простоя 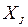 последней между выполнением работ
последней между выполнением работ 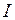 и
и 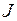 из { АВ }. Даже в том случае, если
из { АВ }. Даже в том случае, если 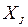 больше, чем длительность выполнения К, эту работу можно выполнить до
больше, чем длительность выполнения К, эту работу можно выполнить до 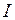 , так как в худшем случае
, так как в худшем случае 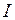 будет задержано,
будет задержано, 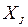 уменьшится, но момент начала выполнения
уменьшится, но момент начала выполнения 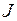 останется прежним и, следовательно, не изменится максимальная длительность прохождения. Аналогичные рассуждения устанавливают оптимальность упорядочения для машины 1.
останется прежним и, следовательно, не изменится максимальная длительность прохождения. Аналогичные рассуждения устанавливают оптимальность упорядочения для машины 1.
 2020-05-12
2020-05-12 939
939