2020-05-12
87
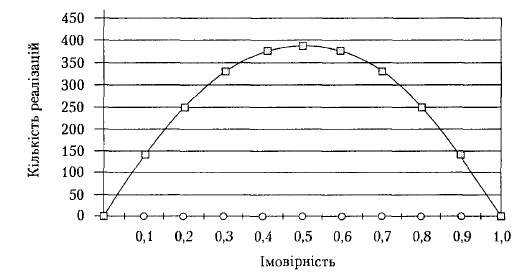
Вероятность
Рис. 2. Зависимость числа реализаций от значений вероятности
Оценка среднего значения
Пусть случайная величина имеет математическое ожидание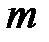 
и дисперсию 
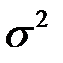. В 
-й реализации она принимает значение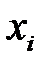 
. В качестве оценки математического ожидания 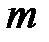используем среднее арифметическое:
(7)
В соответствии с центральной предельной теоремой при больших значениях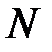 
среднее арифметическое (7) будет иметь нормальное распределение с математическим ожиданием 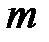и дисперсией 
. Тогда
.
Откуда
(8)
Поскольку дисперсия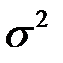 
случайной величины неизвестна, нужно провести несколько десятков (50,…,100) испытаний и найти оценку 
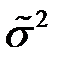, а потом полученное значение подставить в формулу (8), чтобы определить необходимое количество реализаций 
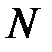. В этом случае вместо нормально распределенной величины необходимо воспользоваться 
-распределением Стьюдента с 
степенями свободы для определения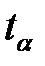 
. С практической точки зрения, если 
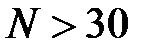пользуются нормальным распределением.
|
|
|
