2020-05-12
76
Для оценки математического ожидания случайной величины используется формула:
,
где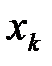 
– значения случайной величины, которые принадлежат 
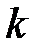– му интервалу; 
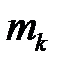– количество попаданий значений случайной величины в интервал; 
– общее количество испытаний.
Чтобы предотвратить ненужную загруженность памяти компьютера, сумму целесообразно подсчитывать путём поступательного накопления.
Оценка дисперсии
Для оценки дисперсии случайной величины используется формула:
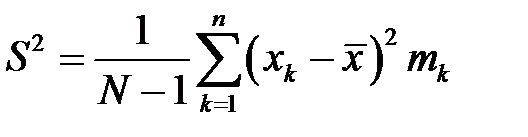
где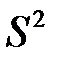 
– оценка дисперсии случайной величины 
.
Непосредственно использовать эту формулу в расчетах дисперсии нерационально, т.к. с увеличением количества значений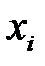 
изменяется также среднее, а для его вычисления нужно хранить в памяти все значений 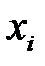. Поэтому на практике для оценки дисперсии пользуются формулой:
.
У этом случае достаточно накапливать только суммы двух последовательносте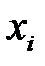й — и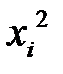 
. Однако и такой способ имеет недостаток – его использование может привести к переполнению разрядной сетки компьютера. Чтобы предотвратить это, нужно изменить последовательность действий при вычислениях, используя формулу:
.
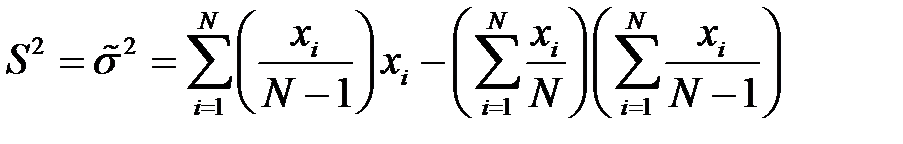Оценка корреляционного момента
Для оценки корреляционного момента можно использовать формулу:
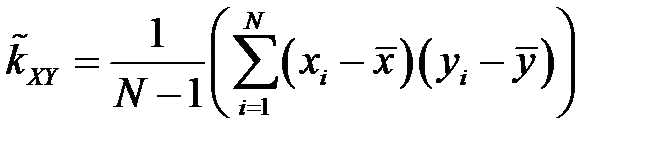
или, более удобную для вычислений,
.
