Определение количества реализаций при моделировании

Точность оценок параметров системы, которые получают во время обработки результатов моделирования, в первую очередь зависит от количества испытаний . Следует учитывать, что объём выборки  всегда ограниченный, поэтому оценки будут иметь разные ошибки и дисперсии.

Если необходимо оценить значения некоторого параметра 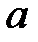 по результатам моделирования 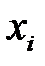, то за его оценку следует брать величину , которая является функцией всех значений 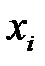. Статистическая оценка  также является случайной величиной, поэтому она будет отличаться от 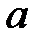, т.е.

где 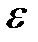 – точность или ошибка оценки. Вероятность того, что это неравенство выполняется, обозначим через :

.

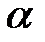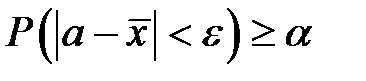В теории вероятностей  — это доверительный интервал для 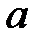, длина которого фактически равн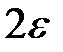а , а 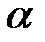 — доверительный уровень, или надёжность оценки. Последнее выражение можно применять для определения точности результатов статистических испытаний.

Оценка вероятности

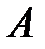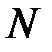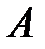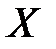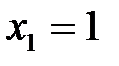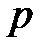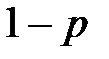Оценим вероятность наступления некоторого события , которое определяет состояние системы. В каждой из  реализаций процесс наступления события  является случайной величиной , которая принимает значения  с вероятностью  и  с вероятностью . Тогда можно определить математическое ожидание и дисперсию случайной величины  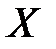соответственно по формулам:

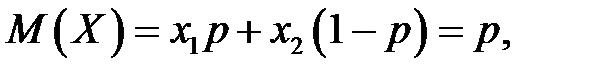                                                                              (2)

(3)

Для оценки вероятности 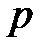 используют абсолютную частоту наступления события 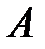. Эта оценка является несмещённой, эффективной и состоятельной. При условии, что  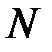задано для получения этой оценки достаточно накапливать :

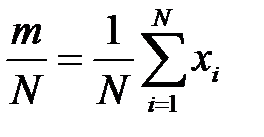                                                        (4)

где 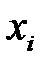 – наступление события  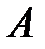в реализации .

По формулам (2)–(4) определим выборочное математическое ожидание 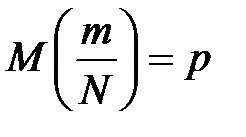 и дисперсию .

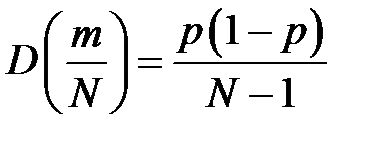По центральной предельной теореме случайная величина  будет иметь распределение, близкое к нормальному распределению (Рис. 1).

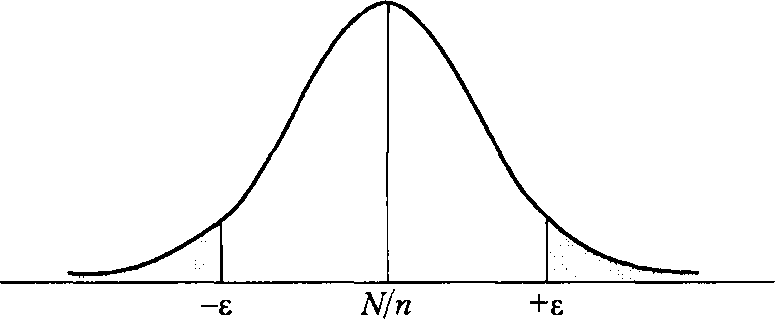
Рис. 1. Функция нормального распределения для построения доверительного интервала

Поэтому для каждого уровня достоверности 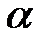 из таблицы нормального распределения можно найти такую величину , при которой точность вычисляется по формуле:

                                   (5)

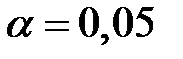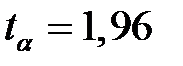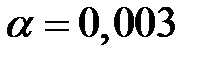Если , то , , то .

Подставим в формулу (5) выражение дисперсии:

.

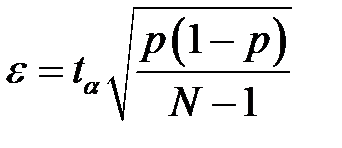Откуда

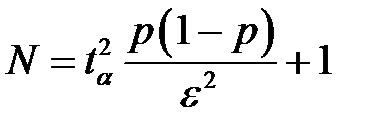                                        (6)

Из формулы (6) видно, что пр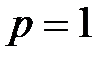и  или 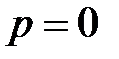, количество реализаций, которые необходимо провести для подтверждения того, что событие  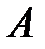наступает (или не наступает), равно единице. Но поскольку вероятность  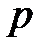наперед неизвестна, проводят испытания ( 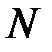=50,..., 100), оценивают абсолютную частоту  и подставляют её значение в выражение (6) вместо 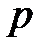, после чего определяют остаточное количество реализаций. График зависимости числа реализаций для  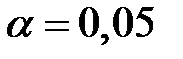и разных значений 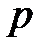, если 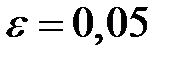, приведен на рис. 2.