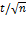Обработка результатов испытаний

 

Результаты испытаний обрабатывают методами математической статистики. Вычисляют среднее арифметическое результатов испытаний:

 

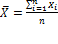                                               (1)

 

где Xi - отдельное значение определяемого показателя i изменяется от 1 до n;

n - количество образцов.

Оценку среднего квадратического отклонения результатов испытаний (S) вычисляют по формуле:

 

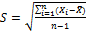                                           (2)

 

Коэффициент вариации результатов испытания (ν) в процентах вычисляют по формуле:

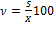                                              (3)

 

Границы доверительного интервала, в котором с вероятностью Р заключено значение показателя  вычисляют по формулам:

 

для нижней границы:		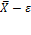(4)
для верхней границы:		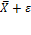(5)

 

где ε - значение, равное половине доверительного интервала.

Величину (ε) вычисляют по формуле:

 

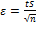                                                  (6)

 

где t - критерий точности (табл. 3).

 

Таблица 3

Значения t и 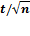 для расчета доверительного интервала среднего

Арифметического значения

Количество образцов, n	t
	Р = 95 %	Р = 99 %	Р = 95 %	Р = 99 %
2	12,71	63,66	9,00	45,01
3	4,30	9,93	2,48	5,73
4	3,18	5,84	1,59	2,92
5	2,78	4,60	1,24	2,06

 

Относительное отклонение (β) в процентах вычисляют по формуле

 

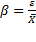                                                (7)

 

В таблице 4 приведены показатели основных механических свойств наиболее распространенных видов пластмасс (справочно): плотность, пределы прочности при разрыве, изгибе и сжатии, относительное удлинение при разрыве и ударная вязкость (KCU).

 

Таблица 4