Вероятность произведения зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое произошло

Теоремы умножения вероятностей

Прежде чем рассматривать следующие теоремы, необходимо ввести еще несколько важных понятий теории случайных событий.

Если при использовании теорем сложения вероятностей проверяется совместность/несовместность событий, то применение теорем умножения требует проверки случайных событий на зависимость/независимость.

· События А и В называются зависимыми, если вероятность одного из них зависит от наступления или не наступления другого. Иначе случайные события называются независимыми.

Пример 2.2. При подбрасывании 2-х монет событие А – появление герба на 1-й монете и событие В – появление герба на 2-й монете - есть события независимые друг от друга, так как вероятность их наступления не зависит от появления или не появления другого события.

При подбрасывании одной и той же монеты несколько раз появление герба каждый раз не зависит от того, появился ли герб предыдущий раз, и соответствующие события также будут независимыми.

Пример 2.3. При извлечении без возвращения одного за другим 2-х шаров из урны с k черными и / белыми шарами событие А – появление первого белого шара и событие В – извлечение после этого второго белого шара – являются зависимыми, так как вероятность события В зависит от того, произошло или нет событие А, изменяющее количество и состав шаров в урне.

· Несовместные события зависимы, так как появление любого из них обращает в нуль вероятности появления всех остальных.

В случае зависимых событий вводится понятие условной вероятности[1].

· Условной вероятностью Р(А\В) события А называется его вероятность, вычисленная при условии, что событие В произошло. Аналогично, через Р(В\А) обозначается условная вероятность события В при условии, что А наступило.

· Для независимых событий по определению Р(А\В)=Р(А); Р(В\А)=Р(В).

Пример 2.4. Из полной колоды карт (52 шт.) случайным образом извлекается одна карта. Определим случайные события, появление

А — дамы,

В – карты черной масти,

С – пиковой дамы,

D – короля.

Определить зависимость/независимость следующих пар событий:

1) А и В; 2) А и С; 3) В и С; 4) В и D; 5) А и D, 6) С и D.

Решение.

1) А и В – независимы, так как

2) А и С – зависимы, так как

3) В и С – зависимы, так как

4) В и D – независимы, так как

5) А и D – зависимы, так как несовместны.

6) С и D – зависимы, так как несовместны.

Теорема умножения для зависимых событий.

Вероятность произведения зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое произошло.

Р(А*В)=Р(А)*Р(В\А) или Р(А*В) = Р(В)*Р(А\В) (1.19)

(в зависимости от того, какое событие произошло первым).

Доказательство.

Пусть событию А благоприятствует , событию В — 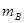, а событию А*В — событий системы S. Очевидно, что выполняются неравенства Если обозначить через N число всех возможных случаев, то согласно классическому определению вероятности (1.3):

Если событие А произошло, то осуществился один из случаев, ему благоприятствующих, тогда событию В благоприятствуют и только случаев, благоприятствующих А*В. Следовательно, Аналогично, Подставляя соответствующие обозначения в очевидные равенства: