
47
Пусть точка движется по криволинейной траектории и в момент времени  она занимает положение
она занимает положение  и имеет скорость
и имеет скорость 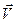 , а в момент
, а в момент  - положение
- положение 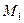 и имеет скорость
и имеет скорость  . Длину элементарной дуги
. Длину элементарной дуги  обозначим
обозначим 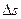 .
.
Представив скорость, как  и учитывая зависимость (26) получаем выражение для ускорения
и учитывая зависимость (26) получаем выражение для ускорения  .
.
Выясним кинематический смысл слагаемых правой части. С первой составляющей все понятно, модуль этого составляющего ускорения равен  и направлен этот вектор по направлению орт вектора
и направлен этот вектор по направлению орт вектора  , т.е. по касательной. Эта составляющая ускорения называется касательным или тангенциальным ускорением и обозначается
, т.е. по касательной. Эта составляющая ускорения называется касательным или тангенциальным ускорением и обозначается
 (37)
(37)
Рассмотри вторую составляющую, т.е. определяем модуль и направление вектора  .
.  , где
, где  - разность векторов
- разность векторов 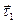 и
и  , построенных в точках
, построенных в точках 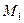 и
и  . Чтобы найти вектор
. Чтобы найти вектор  перенесем вектор,
перенесем вектор, 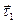 не изменяя его направления из точки
не изменяя его направления из точки 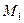 в точку
в точку  . Соединив концы векторов
. Соединив концы векторов 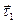 и
и  , достроим
, достроим  до параллелограмма
до параллелограмма  (рис. 54). Вектор
(рис. 54). Вектор  представляет собой разность векторов
представляет собой разность векторов 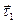 и
и  , т.е.
, т.е.
 .
.
Разделив  на промежуток времени
на промежуток времени  получим новый вектор
получим новый вектор  , направленный по прямой
, направленный по прямой  . Выясним направление этого вектора в пределе при
. Выясним направление этого вектора в пределе при  . Как было указано в предыдущем параграфе, плоскость параллелограмма
. Как было указано в предыдущем параграфе, плоскость параллелограмма  в пределе при
в пределе при  превращается в соприкасающуюся плоскость траектории в точке
превращается в соприкасающуюся плоскость траектории в точке  . Отсюда следует, что вектор
. Отсюда следует, что вектор  лежит в соприкасающееся плоскости.
лежит в соприкасающееся плоскости.
Найдем величину угла между векторами  и
и  , т.е. угол
, т.е. угол  . Треугольник
. Треугольник  является равнобедренным, т.к.
является равнобедренным, т.к.  ,
,  (рис. 55). Угол при вершине
(рис. 55). Угол при вершине  равен углу смежности
равен углу смежности  . Получаем
. Получаем  , а поэтому
, а поэтому  . Отсюда заключаем, что в пределе при
. Отсюда заключаем, что в пределе при  угол
угол  становится прямым, а следовательно направление вектора
становится прямым, а следовательно направление вектора  совпадает с положительным направлением главной нормали, т.е. с направлением орт вектора
совпадает с положительным направлением главной нормали, т.е. с направлением орт вектора  , значит
, значит
48
 . Определяем модуль этого вектора
. Определяем модуль этого вектора  . Из треугольника
. Из треугольника  (рис.18)
(рис.18)  , тогда
, тогда  . Переходим к пределу
. Переходим к пределу
 . Тогда
. Тогда  .
.
 . Окончательно
. Окончательно  . Тогда
. Тогда  . Этот вектор также полностью определен, по модулю он равен
. Этот вектор также полностью определен, по модулю он равен  и направлен по главной нормали к центру кривизны, с учетом орт вектора
и направлен по главной нормали к центру кривизны, с учетом орт вектора  . Эта составляющая ускорения называется нормальным или центростремительным ускорением и обозначается
. Эта составляющая ускорения называется нормальным или центростремительным ускорением и обозначается
 (38)
(38)
Оба вектора  и
и  лежат в соприкасающейся плоскости, значит и итоговый вектор
лежат в соприкасающейся плоскости, значит и итоговый вектор  лежит в этой же плоскости, а проекция этого вектора на бинормаль равна нулю
лежит в этой же плоскости, а проекция этого вектора на бинормаль равна нулю  .
.
 (39)
(39)
Т.о. проекция ускорения на направление скорости равна производной от модуля скорости по времени, а проекция ускорения на главную нормаль равна отношению квадрату скорости к радиусу кривизны траектории в той же точке, где в данный момент находится движущаяся точка.
Рассмотрим как определяется ускорение точки для частных случаев движения.
1. Равномерное прямолинейное движение.
 ,
,  ,
,  ,
,  ,
, 
2. Неравномерное прямолинейное движение.
 ,
,  ,
,  ,
,  ,
,  ,
, 
3. Равномерное криволинейное движение.
 ,
,  ,
,  ,
,  ,
,  ,
, 
Неравномерное криволинейное движение.
49
 ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Используя связь между координатным и естественным способами задания движения точки, можно вывести зависимости, связывающие проекции ускорения на естественные и декартовые оси. Из зависимости (37)
 (40)
(40)
Из зависимости (38), с учетом (32) и (39), получаем выражение для нормального ускорения точки
 (41)
(41)
Из зависимости (38) с учетом (41), получим выражение для радиуса кривизны
 (42)
(42)
 2020-05-12
2020-05-12 665
665








