Кривизна, радиус кривизны траектории

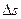    Пусть нам дана некоторая кривая (траектория точки), изображенная на рисунке 50. Возьмем на ней две близкие точки  и , и длину дуги  обозначим через . Проведем в точках  и  касательные к данной кривой. Угол между касательными, называемый углом смежности и измеряемый в радианах обозначим . Отношение  называется средней кривизной дуги  .

Предел, к которому стремится средняя кривизна дуги , когда точка  неограниченно приближается к точке , называется кривизной данной линии в точке . Если обозначить кривизну через , то получаем:

                                                                                         (34)

                      Величина обратная кривизне называется радиусом кривизны данной кривой в точке . Обозначим радиус кривизны через , тогда

                                             или                                         (35)

    Рассмотрим частные случаи, чему равен радиус кривизны для прямой линии и окружности радиуса .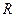

а) Для прямой линии кривизна равна нулю , , .

45

б) Для окружности радиуса 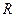 (рис. 51). , но , , тогда .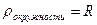

    Получили, что радиус кривизны окружности равен ее радиусу. Отсюда замечаем, что радиус кривизны кривой линии есть радиус такой окружности, которая имеет с данной кривой в данной точке одинаковую кривизну.

    Если траектория точки есть плоская кривая, заданная уравнением , то радиус кривизны в произвольной точке этой кривой можно определить по общей формуле, которая выводится в дифференциальном исчислении

                                                                                                                    (36)