Векторные диаграммы для представления

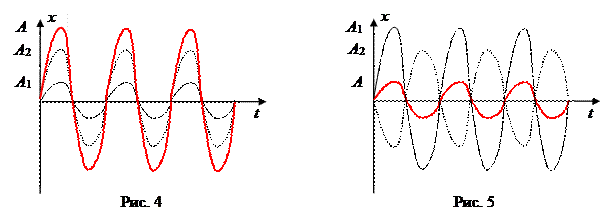
Гармонических колебаний

Рис. 8

х =А cos(w₀ t + j).

.              

 

Сложение параллельных колебаний

Одинаковой частоты. Биения.

 

х ₁ = А ₁ cos (w₀ t + j₁),

(1)

x ₂ = A ₂ cos (w₀ t+ j₂).

 

х = х ₁ + х ₂ .             (2)

, (3)

  

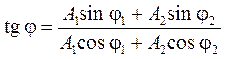. (4)

Частные случаи

1. Колебания совпадают по фазе: j₂ - j₁ = 0

А = А ₁ + А ₂ .

2. Колебания находятся в противофазе a₂ - a₁ =    .

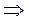
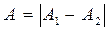Особый интерес представляет случай, когда два складываемых гармонических колебания мало отличаются по частоте. Результирующее движение при этих условиях можно рассматривать как гармонические колебания с пульсирующей амплитудой. Такие колебания называются биением.

 

x ₁ = A cos w t,     x ₂ = A cos (w + Dw) t.     Dw << w.                      (5)

 

 

                                 (6)

 

Амплитуда и частота биений

,   .                                 (7)                            

 

            

Вынужденные колебания. Резонанс

 

Колебательная система подвергается действию внешней вынуждающей силы, изменяющейся со временем по гармоническому закону:

F_x = F ₀sinW t.         (1)

 

 

Рис. 2

 

Вынужденные колебания – это незатухающие колебания. Существуют системы, в которых незатухающие колебания возникают не за счет периодического внешнего воздействия, а в результате имеющейся у таких систем способности самой регулировать поступление энергии от постоянного источника. Такие системы называются автоколеба­тель­ными, а процесс незатухающих колебаний в таких системах – автоколебаниями.