Расчет вала на жесткость

Размеры вала, определенные расчетом на прочность, не всегда обеспечивают достаточную его жесткость, необходимую для нормальной работы зубчатой передачи (перекос зубчатых колес и концентрация нагрузки по длине зуба) и подшипников (защемление тел качения). Валы редукторов обычно выдерживают проверку на жесткость, но валы червяков всегда проверяют на изгибную жесткость для обеспечения правильности зацепления.

Изгибная жесткость обеспечивается при выполнении условия:

,

где     – допускаемый прогиб вала.

Допускаемый прогиб  рекомендуется принимать в зависимости от модуля зацепления по соотношению для валов червячных передач: .

При симметричном расположении опор относительно прилагаемой к зубчатому колесу нагрузки (наиболее типичном для одноступенчатых редукторов) прогиб (стрела прогиба) вала червяка определяется из выражения:

где Е   –   модуль продольной упругости (для стали Е  =  2,1∙10⁵ МПа);

I _пр– приведенный момент инерции сечения червяка, мм⁴

Если жесткости вала червяка недостаточно, увеличивают коэффициент диаметра червяка q и повторяют расчеты и построения элементов червячной передачи.

 

Пример 1. Проверить тихоходный вал цилиндрического косозубого редуктора на сопротивление усталости. Опасное сечение вала – под колесом (), концентратор напряжений – шпоночный паз. Материал вала – сталь 45.

Исходные данные: механические характеристики стали: =900 МПа, =650 МПа, =410 МПа, =230 МПа, 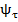=0,10. Размеры шпоночного паза: b = 18 мм, t ₁ = 7 мм. Изгибающий момент с суммарной эпюры =69,3 Н∙м. Крутящий момент на валу =140 Н∙м.

1. Вычислим значения напряжений цикла:

где W_x – момент сопротивления изгибу, мм³ (табл. 48):

W _r – момент сопротивления кручению, мм³ (табл. 48):

Тогда                    

81

2. Для опасного сечения вала выпишем значения коэффициентов:

– коэффициенты снижения предела выносливости за счет местных концентраторов напряжений (табл. 51, 52):

– коэффициент влияния абсолютных размеров (табл. 50): ;

– коэффициент влияния обработки поверхности (табл. 53): ;

– коэффициент упрочнения поверхности: так как поверхность вала не подвергается упрочнению, то .

3. Вычислим коэффициенты концентрации нормальных и касательных напряжений:

4. Вычислим запас прочности вала по нормальным и касательным напряжениям:

5. Рассчитаем общий коэффициент запаса прочности в сечении при совместном действии изгиба и кручения:

 – условие прочности вала выполняется.

 

82