Согласно второму началу термодинамики, элементарное количество теплоты 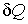 связано с изменением энтропии системы
связано с изменением энтропии системы 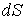 следующим неравенством (см. формулу (3.59)):
следующим неравенством (см. формулу (3.59)):
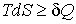 . .
| (4.1) |
Совместно с первым началом термодинамики
 , ,
| (4.2) |
выражение (4.1) дает основное неравенство термодинамики в виде:
 . .
| (4.3) |
В этом выражении знак равенства соответствует равновесным термодинамическим процессам, а знак неравенства - неравновесным.
Для анализа равновесных процессов выражение (4.3) может быть записано в виде уравнения
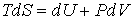 , ,
| (4.4) |
которое носит название основного уравнения термодинамики равновесных (обратимых) процессов. Уравнение (4.4) позволяет проводить расчет любых равновесных термодинамических процессов.
Рассмотрим применение этого уравнения для определения соотношения между уравнением состояния  и выражением для внутренней энергии
и выражением для внутренней энергии 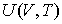 термодинамической системы. Преобразуем выражение (4.4) к следующему виду:
термодинамической системы. Преобразуем выражение (4.4) к следующему виду:
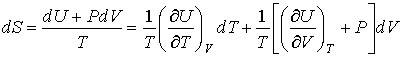 . .
| (4.5) |
Здесь учтено, что внутренняя энергия  является функцией состояния, и поэтому она имеет полный дифференциал:
является функцией состояния, и поэтому она имеет полный дифференциал:
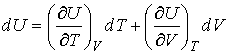 . .
| (4.6) |
С другой стороны, так как энтропия 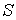 тоже является функцией состояния, для ее полного дифференциала можно записать выражение:
тоже является функцией состояния, для ее полного дифференциала можно записать выражение:
 . .
| (4.7) |
Сопоставление формул (4.5) и (4.7) дает
 , ,
| (4.8) | ||
|
| (4.9) | ||
Далее, учитывая то, что
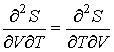
| (4.10) |
и дифференцируя по 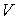 выражение (4.8) и по
выражение (4.8) и по 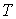 выражение (4.9), имеем:
выражение (4.9), имеем:
 . .
| (4.11) |
Использование равенства
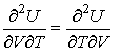
| (4.12) |
позволяет получить окончательное выражение для дифференциального уравнения, связывающего уравнение состояния 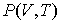 и внутреннюю энергию
и внутреннюю энергию  термодинамической системы
термодинамической системы
 . .
| (4.13) |
Рассмотрим применение этого уравнения для определения внутренней энергии идеального газа, для которого уравнение состояния имеет вид
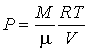 . .
| (4.14) |
Подстановка формулы (4.14) в уравнение (4.13) дает
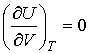 . .
| (4.15) |
Таким образом, внутренняя энергия идеального газа не зависит от его объема, а является функцией только его температуры:
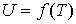 . .
| (4.16) |
Так как внутренняя энергия идеального газа пропорциональна количеству вещества 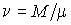 , а его молярная теплоемкость
, а его молярная теплоемкость 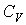 не зависит от температуры, то с точностью до произвольной постоянной имеем
не зависит от температуры, то с точностью до произвольной постоянной имеем
 . .
| (4.17) |
Подстановка полученного выражения для внутренней энергии идеального газа и его уравнения состояния в основное уравнение термодинамики равновесных процессов, записанного в виде (4.5), дает
 . .
| (4.18) |
Интегрирование этого уравнения позволяет определить зависимость энтропии идеального газа от его объема и температуры 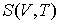 :
:
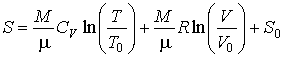 , ,
| (4.19) |
где: 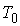 ,
, 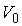 и
и 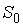 – константы, имеющие размерности температуры, объема и энтропии соответственно.
– константы, имеющие размерности температуры, объема и энтропии соответственно.
Выражение (4.19) полностью совпадает с формулой (3.65). Оно позволяет рассчитывать энтропию идеального газа при достаточно высоких температурах.
 2020-05-11
2020-05-11 210
210
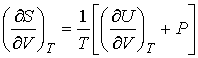 .
.






