Практическое занятие № 12

Тема: Геометрический смысл производной

Цель: Формирование умений анализа условия задачи, выделения главного вопроса задачи, конструирования способа решения на основе имеющихся знаний по теме: «Геометрический смысл производной»

Методические указания.

Геометрически производная у' функции  представляет угловой коэффициент касательной к графику этой фун­кции в соответствующей точке tg а = у ^/.

 

Итак, геометрический смысл производной: производная функции в точке равна угловому коэффициенту касательной к графику функции в                                                           этой точке или тангенсу угла наклона касательной к                                                                оси абсцисс.

Содержание работы

№1 Найдите тангенс угла наклона касательной, проведенной к графику функции у, в точке с абсциссой

1. ,

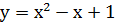2. ,

3. ,

4. ,

№2 Найдите угловой коэффициент касательной, проведенной к графику функции у, в точке с абсциссой

1. ,

2. ,

№ 3

1. На рисунке изображен график функции y= f(x) и касательная к нему в точке с абсциссой . Найдите значение производной функции f(x) в точке

 

2. На рисунке изображен график функции y= f(x) и касательная к нему в точке с абсциссой . Найдите значение производной функции f(x) в точке

 

 

Контрольные вопросы

1. Какой формулой задается линейная функция

2. Вставить пропущенные слова: «Число ____ называют угловым коэффициентом прямой, а угол  - углом между _______________________»

3. Геометрический смысл производной, состоит в том что ___________

4. Какой знак имеет тангенс а) острого угла, б) тупого угла

5. Значение тангенса  равно _______

Практическое занятие № 13

Тема: Уравнение касательной в общем виде

Цель: формирование навыков составление уравнения касательной к графику функции