Тема: Исследование функции с помощью производной.
Цель: ознакомление с понятиями монотонности функции, точками экстремума и экстремумами функции; формирование умения применять полученные знания для исследования функции.
Методические указания.
С помощью производной функции можно определить характер монотонности функции, точки экстремума, а также ее наибольшее и наименьшее значение на заданном промежутке.
Достаточное условие возрастания (убывания) функции:
а) если на заданном промежутке  , то функция возрастает на этом промежутке;
, то функция возрастает на этом промежутке;
б) если  , то функция убывает на этом промежутке.
, то функция убывает на этом промежутке.
Экстремум функции
Максимумом (минимумом) функции 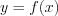 называют такое ее значение, которое больше (меньше) всех ее других значений в окрестности рассматриваемой точки.
называют такое ее значение, которое больше (меньше) всех ее других значений в окрестности рассматриваемой точки.
Максимум и минимум функции имеют локальный характер, поскольку отдельные минимумы некоторой функции могут оказаться больше максимумов той же функции.
Максимум и минимум функции называются экстремумом функции. Значение аргумента, при котором достигается экстремум, называется точкой экстремума. На рисунке значения  ,
,  ,
,  ,
,  и
и  являются точками экстремума рассматриваемой функции.
являются точками экстремума рассматриваемой функции.

Критическими точками функции называют те значения аргумента, при которых производная функции равна нулю или не существует. Критические точки функции находят, решая уравнение:  .
.
Пример 1. Найдите промежутки монотонности и точки экстремума функции  .
.
Решение. Используя таблицу производных найдем производную функции:  . Найдем критические точки:
. Найдем критические точки:  ,
,  ,
, 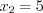 . Нанесем числа
. Нанесем числа  и
и  на координатную прямую и установим знаки производной на полученных промежутках:
на координатную прямую и установим знаки производной на полученных промежутках:
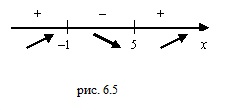
Ответ: На промежутках 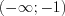 и
и  функция возрастает. На промежутке
функция возрастает. На промежутке  функция убывает. Точки экстремума:
функция убывает. Точки экстремума:  ,
,  .
.
Пример 2. Найдите точки перегиба и промежутки выпуклости и вогнутости графика функции 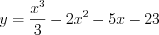 .
.
Решение. 1. Используя таблицу производных найдем первую производную функции:  .
.
2. Используя таблицу производных найдем вторую производную функции:  .
.
3. Найдем критические точки второго рода:  ,
,  .
.
4. Нанесем точку  на область определения данной функции и установим знаки ее второй производной на полученных промежутках:
на область определения данной функции и установим знаки ее второй производной на полученных промежутках:

Ответ: На промежутке  функция выпукла вверх; на промежутке
функция выпукла вверх; на промежутке 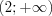 функция выпукла вниз;
функция выпукла вниз;  – точка перегиба графика функции.
– точка перегиба графика функции.
Пример 3. Найдите наибольшее и наименьшее значение функции  на отрезке
на отрезке  .
.
Решение. 1. По формуле  найдем производную данной функции:
найдем производную данной функции:  .
.
2. Найдем критические точки функции, решая уравнение  , откуда
, откуда  ,
, 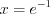 .
.
3. Найдем значение функции на концах отрезка  и в критической точке
и в критической точке 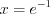 , поскольку она принадлежит данному отрезку:
, поскольку она принадлежит данному отрезку: 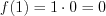 ,
,  ,
,  .
.
Ответ: 
 ,
,  .
.
Содержание работы
№1. Найти промежутки возрастания и убывания функции:
1. y=2x5+4x3-1
2. 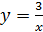
№2. Найти промежутки монотонности функции:
f(x)=2x2-5x=3
№3. Найти наибольшее и наименьшее значения функции
y=2x3+3x2-36x
на отрезке [-2;1]
№4. Найти точки экстремума и экстремумы функции:
y=2x3-9x2+12x-8
Контрольные вопросы
1. Дать определение экстремумов функции.
2. Сформулировать теорему о достаточных условиях монотонности функции.
3. Сформулируйте признак максимума (минимума) функции.
4. Опишите схему исследования функции?
 2020-05-11
2020-05-11 439
439







