Другой способ решения

Другой способ решения

Все три тригонометрические функции содержат аргумент в виде, к которому можно применить правило «головы лошади»:

1.

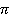находится там же, где , плюс альфа, третья четверть, синус отрицательный (см. рис. 2). Диаметр горизонтальный, лошадь мотает головой, функцию не меняем, получаем:

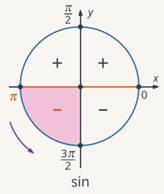
Рис. 2. Иллюстрация к заданию 5

2.

Вторая четверть, косинус отрицательный, диаметр вертикальный (см. рис. 3), меняем функцию, получаем:

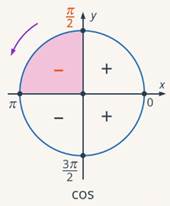
Рис. 3. Иллюстрация к заданию 5

3.

Вторая четверть, синус положительный, диаметр горизонтальный (см. рис. 4), функцию не меняем, получаем:

Рис. 4. Иллюстрация к заданию 5

Тогда:

Задание 6. Вычислить:

Решение

В таблице мы не найдем точного значения . Конечно, можно вычислить приближенное значение с помощью калькулятора:

Аналогично можно поступить с другим тангенсом и вычислить ответ:

Но это лишь приближенное значение. Можно ли найти точное? Обратим внимание, что углы отличаются на . Это дает подсказку, что здесь можно использовать формулы приведения:

В формуле приведения из вычитается альфа, а тут – прибавляется. Как и в предыдущем примере, сделаем из сложения вычитание:

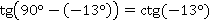
Распишем котангенс по определению, чтобы получить для него формулу приведения:

Тогда:

И это уже будет точный, а не приближенный ответ.

Ответ: .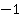

Другой способ решения

Ко второму тангенсу применим формулу приведения (используя правило «головы лошади»): – вторая четверть, тангенс отрицательный, диаметр вертикальный (см. рис. 5), функцию меняем:

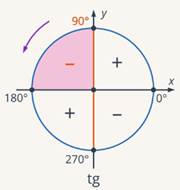
Рис. 5. Иллюстрация к заданию 6

Подведем итоги использования формул приведения.

1. Сначала убираем периоды у функций. Для этого представляем угол в виде:
(или 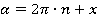) для косинусов и синусов;
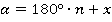(или ) для тангенсов и котангенсов.

2. Выбираем подходящую формулу приведения. При необходимости прибавляем/вычитаем 1 период, заменяем вычитание сложением или наоборот.

3. При наличии тангенсов/котангенсов расписываем их через синус и косинус, к которым применяем формулы приведения. Или же используем готовые формулы приведения для тангенсов и котангенсов.

4. Формулы приведения можно применять и для расчетов. То, что их нужно применить, подскажет следующее: сумма или разность углов будет равна или .

Формулы двойного и половинного аргумента

Теперь перейдем к формулам двойного аргумента и следствиям из них. Напомним:

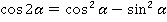
Получить формулы для тангенса и котангенса двойного угла очень просто. Этот прием мы уже неоднократно использовали сегодня в уроке. Расписываем по определению:

По сути, мы получили формулу для тангенса двойного угла. Ее можно преобразовать и к другому виду, разделив числитель и знаменатель на :

Получилась многоэтажная дробь, разберем ее числитель и знаменатель отдельно:

В итоге тангенс двойного угла мы выразили только через тангенс одинарного.

Аналогичным образом можно поступить и с котангенсом.

 

Задание 7. Найти 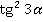, если .

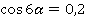Решение

Обратим внимание, что аргументы отличаются в 2 раза. Значит, нам понадобятся формулы двойного угла или же следствия из них – формулы половинного угла.

Способ 1. Попробуем использовать формулы двойного угла:

По условию, это выражение равно :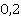

Тут у нас косинус квадрат и синус квадрат. Для них мы знаем еще одно соотношение – основное тригонометрическое тождество:

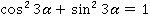
Из этих двух соотношений мы можем найти значения и . Сложив их, получим:

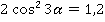
Тогда:

Требуется найти 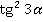. Как обычно, расписываем по определению:

Способ 2. Можно использовать формулы половинного аргумента. Тогда и можно сразу выразить:

Ответ: .

 

Вторым способом получилось быстрее, но нужно помнить больше формул. Каждый сам может выбрать более удобный для себя способ решения: больше запоминать, но быстрее решать или же запоминать меньше, но тогда решение может оказаться длиннее.

 

Уметь применять формулы двойных аргументов нужно как слева направо, так и справа налево. Слева направо это сделать проще, а вот справа налево их нужно «увидеть». Вспомните: похожая ситуация была с формулами сокращенного умножения. Найти выражение вида просто: увидел – применил формулу. А вот в обратную сторону выражение вида 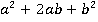нужно еще заметить.

 

Итак, посмотрим на правые части формул двойных аргументов и подумаем, на что же нам обращать внимание.

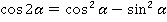
Для синусов справа стоит произведение синуса и косинуса с одинаковыми аргументами. Именно на это мы будет обращать внимание. Умножить и разделить выражение на 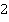– это не проблема. Для косинусов справа стоит разность квадратов. Не путайте с основным тригонометрическим тождеством – там сумма квадратов.

Задание 8. Найти значение выражения:

Решение

Видим произведение косинуса и синуса одного аргумента. Это показатель того, что нужно применить формулу синуса двойного угла. Не хватает двойки перед выражением. Поэтому умножим и разделим выражение на :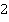

Теперь можем применить формулу:

Далее нужно применить формулы приведения. Можете самостоятельно потренироваться это делать. В итоге вы должны получить ответ . Если ответ не совпал, смотрите решение ниже.

Ответ: .