2020-05-21
92
Найдем условия того, что два числа являются косинусом и синусом некоторого угла.
Для произвольного угла мы давали определение его синуса и косинуса – это координаты соответствующей точки на единичной окружности (см. рис. 1).
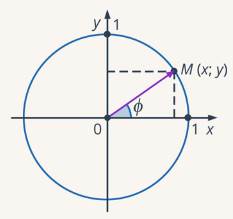
Рис. 1. Синус и косинус произвольного угла – это координаты соответствующей точки на единичной окружности
Верно и обратное: если мы возьмем точку на единичной окружности, то ее координаты – это будут синус и косинус соответствующего угла. Точнее, многих углов – с точностью до периода. Значит, если пара чисел – это координаты точки на единичной окружности, то эти числа будут косинусом и синусом некоторого угла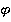 
.
А какое условие, что точка лежит на единичной окружности? Сумма квадратов ее координат должна равняться 
(уравнение окружности: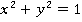 
). Вот и получили условие. Проверим его для выражений 
и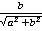 
:
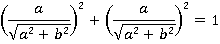
Возводим в квадрат:
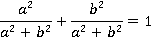
Равенство верное. Значит, всегда найдется такой угол 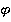, что:
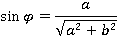
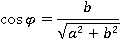
Естественно, это не случайность – мы специально так выбрали выражения, чтобы сумма их квадратов была равна 1.
|
|
|
Преобразования суммы тригонометрических функций в произведение и наоборот
В конце нашего занятия мы поговорим о формулах преобразования суммы тригонометрических функций в произведение и наоборот. Как и все предыдущие, они также применяются для упрощения выражений. Конечно, у вас может возникнуть вопрос: «Во что преобразовывать, чтобы упростить выражение: в сумму или в произведение?». Если у вас такой вопрос возник, вспомните, как поступать в таких же ситуациях с рациональными выражениями: когда раскладывать на множители, а когда – раскрывать скобки.
Задание 11. Упростить выражение:
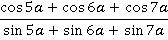
Решение.
Упростить дробь – значит ее сократить. Для сокращения дроби нужно разложить числитель и знаменатель на множители. То есть нужно преобразовать сумму в произведение. Тут у нас по 3 слагаемых, какие же складывать? Возможны различные варианты, но начинать всегда лучше с симметричных. То есть со сложения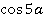 
и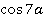 
и аналогичных синусов:
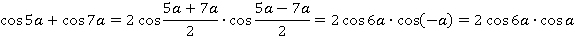
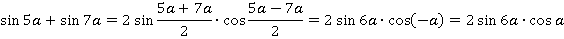
Подставим в исходное выражение:
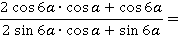
Теперь тут есть общие множители, которые можно вынести за скобки:
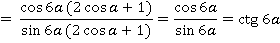
Ответ: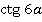 
.
Задание 12. Доказать тождество:
Решение.
Для доказательства упростим левую часть равенства и покажем, что она всегда равна правой. Здесь по порядку действия стоит сначала умножение, затем – сложение. Поэтому сначала можем преобразовать только произведение в сумму:
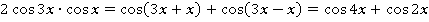
Подставив в левую часть равенства, получим:
Видим, что после упрощения левая часть равенства тождественно равна правой.
Доказано.
