Вывод формул тангенса суммы и разности

По определению:

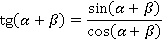
Применяем формулы косинусов и синусов суммы:

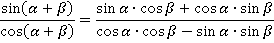
Разделим числитель и знаменатель на 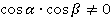. В числителе получим:

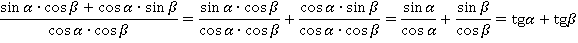
В знаменателе:

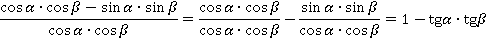
В итоге:

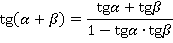
Чтобы получить формулу разности, запишем:

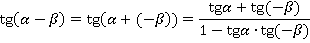
С учетом формул приведения:

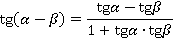
Как и другие формулы, формулы косинусов и синусов суммы и разности могут помочь при упрощении выражений.

Задание 9. Упростить выражение:

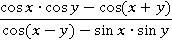
Решение.

Применяем формулы косинуса суммы и разности:

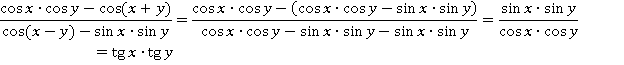
Ответ: .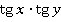

 

У формулы синуса суммы есть еще один, совсем не очевидный способ применения.

Задание 10. Упростить выражение:

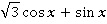
Решение.

Казалось бы: куда же еще упрощать, тут всего 4 операции для вычисления? Но это можно сделать. Вынесем за скобку число 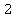. Да, в выражении его нет. Но это не мешает нам каждое слагаемое умножить и поделить на :

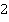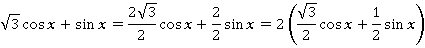
Пока не проще. Но подождите: 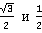– это значения косинусов и синусов из таблицы. Например:

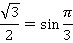
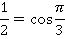
Тогда наше выражение равно:

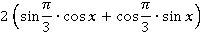
В скобках мы видим синус суммы. Получаем ответ:

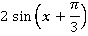
Ответ: .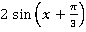

Это выражение действительно проще – в нем всего 3 операции: сложение, вычисление синуса, умножение.

Данный прием может пригодиться не только при упрощении выражений, но и при решении уравнений, оценке значений, построении графиков. В общем виде его можно представить так.

Пусть имеется выражение вида:

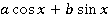
Выносим за скобки выражение :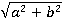

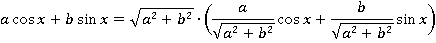
При этом всегда можно найти такой угол 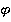, что:

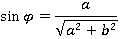
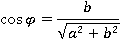
Тогда получим:

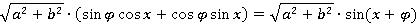
О том, почему всегда найдется такой угол 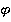, смотрите ниже.