2020-05-21
103
Лекция: представление булевых функций
Формулы. Реализация булевых функций формулами. Принцип двойственности.
Как и в обычной алгебре на базе элементарных функций строятся формулы, определяемые индуктивно. Пусть 
– подмножество булевых функций. Тогда а) каждая 
является формулой над F; б) если и 
– формулы над F или символы булевых переменных, то выражение 
также является формулой над F.
При построении формул применяются переменные, связки 
и скобки (при опускании некоторых из них связка 
считается самой сильной, а 
– сильнее любой другой двухместной связки). Запись 
означает, что 
построена на функциях 
, а запись 
указывает на переменные, используемые в .
Формулы 
и 
имеют одинаковое строение 
, если 
получена из 
путем замены 
.
Формуле над F по индукции сопоставим булеву функцию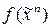 
: а) если 
, то реализует ; б) если 
, где 
– формулы над F или переменные, то реализует функцию 
, где 
при 
либо переменная, либо 
.
Формулы, реализующие равные функции называются эквивалентными.
Функция f, реализуемая формулой , называется суперпозицией функций из F. Строение формулы можно описать помеченным деревом. Так, формуле 
соответствует дерево
Определение 1. Функция 
называется двойственной к функции 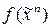, если имеет место равенство 
. 
.
Интерпретация двойственной функции с помощью таблицы.
Примеры. 0 двойственна 1; 
– ; 
– ; 
– 
;
– 
; 
– 
.
Справедлив следующий принцип двойственности.
Теорема 1. Если f реализуется формулой 
, то 
– 
, имеющей такое же строение, как и формула .
Доказательство. Добавляя, если нужно, несущественные переменные, по определению имеем 
,
Таким образом, получили 
, ч. т. д.
С помощью этого принципа легко строится формула, реализующая функцию, двойственную к заданной функции. Пример: законы дистрибутивности, формулы де Моргана, правила поглощения и т. д.
Разложение булевых функций по переменным. Совершенная ДНФ и совершенная КНФ.
Для булевой переменной x и булевого параметра s определим функцию
или 
.
Теорема 1. (О разложении функции по множеству переменных) Каждую 
при 
можно представить в следующей форме:
,
где дизъюнкция берется по всем наборам переменных 
.
Доказательство. Вместо 
подставим набор 
и получим равенство.
Замечание. В теореме 1 функцию 
можно заменить функцией 
.
Следствие 1. При 
имеем разложение по переменной 
.
Следствие 2. При 
имеем представление
,
называемое совершенной ДНФ (ДНФ – дизъюнктивная нормальная форма), причем функцию 0 нельзя представить в виде совершенной ДНФ.
Замечание. В следствии 2 функцию можно заменить .
Таким образом, каждую булеву функцию можно реализовать формулой над множеством связок 
или 
.
Следствие 3. Каждая булева функция, кроме 1, имеет представление
,
называемое совершенной КНФ (КНФ – конъюнктивная нормальная форма).
Доказательство. Для функции 
совершенная ДНФ имеет вид
,
а для двойственной функции к получим
.
Так как 
и
,
то получим требуемое выражение в виде совершенной КНФ.
