2020-05-21
150
Теорема 1. Каждая булева функция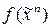 
единственным образом представима в виде полинома по 
(полинома Жегалкина):
,
где суммирование проводится по всем подмножествам 
множества 
(их число 
), а коэффициенты принимают значения из 
.
Доказательство. Преобразуя формулу для функции 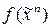над множеством связок 
заменой 
и упрощением с помощью равенств 
получим полином Жегалкина. Так как таких полиномов 
, то каждой 
отвечает один полином Жегалкина.
Полином Жегалкина можно построить несколькими способами:
а) Преобразование формул над множеством связок 
. В этом методе строится формула Ф над , реализующая данную функцию f. В Ф заменяются подформулы вида 
на 
, раскрываются скобки с помощью тождества 
и проводится упрощение с использование равенств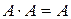 
, 
, 
(для формулы над множеством связок 
можно использовать равенство 
).
б) Метод неопределенных коэффициентов использует табличное задание функции f и теорему 3.
в) Метод преобразования вектора значений функции [4.6] обычно содержит наименьшее количество операций преобразования.
|
|
|
г) Применение формулы
.
Примеры. а) 
.
б) 
.
г)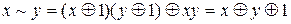 
.
Неполностью определенные (частичные) булевы функции принимают значения из множества 
, где "–" означает неопределенное значение.
Виды ДНФ и КНФ
Формулы 
, 
называются, соответственно, элементарной конъюнкцией и дизъюнкцией, если каждая буква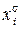 
входит в них не более одного раза, а число r букв вида 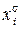называется их рангом.
Формулы 
и 
называются соответственно ДНФ и КНФ, если элементарные конъюнкции (дизъюнкции) в них попарно различны, а число l элементарных конъюнкций (дизъюнкций) называется их длиной. Сумма рангов всех конъюнкций (дизъюнкций), входящих в ДНФ (КНФ), называется сложностью ДНФ (КНФ). Совершенная ДНФ (КНФ) функции 
составлена из элементарных конъюнкций (дизъюнкций) ранга n.
Определение 1. ДНФ называется минимальной, если она содержит наименьшее число букв среди всех ДНФ, эквивалентных ей.
Определение 2. ДНФ называется кратчайшей, если она имеет наименьшую длину среди всех ДНФ, эквивалентных ей.
Можно показать, что минимальная ДНФ является кратчайшей, но обратное неверно.
При упрощении ДНФ используются две простые операции: а) удаление элементарной конъюнкции K, б) удаление буквы 
.
ДНФ называется тупиковой, если применение к ней любой из операций а), б) приводит к ДНФ, не эквивалентной исходной.
Определение 3. Импликантой функции называется элементарная конъюнкция K, обладающая свойством: 
. Она называется простой, если удаление из нее любой буквы приводит к конъюнкции, не являющейся импликантой функции .
Определение 4. Дизъюнкция всех простых импликант функции f называется сокращенной ДНФ функции f.
|
|
|
Определение 3*. Имплицентой функции называется элементарная дизъюнкция D, обладающая свойством: 
. Она называется простой, если удаление из нее любой буквы приводит к дизъюнкции, не являющейся имплицентой функции .
Определение 4*. Конъюнкция всех простых имплицент функции f называется сокращенной КНФ функции f.
Говорят, что f поглощает функцию g, если 
(или 
).
Пусть для функции 
– множество вершин единичного куба 
, 
. Импликанте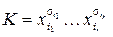 
функции f отвечает множество 
, 
, являющееся гранью единичного куба. Эта грань ранга r имеет размерность 
и называется интервалом функции 
, соответствующим импликанте K. В частности, вершина куба – интервал размерности 0, ребро – размерности 1 и т. д.
Определение 5. Интервал функции 
, не содержащийся ни в каком другом интервале функции , называется максимальным интервалом. Максимальные интервалы функции соответствуют ее простым импликантам, а интервалы, соответствующие ядровым импликантам, называются ядровыми.
