При построении сокращенной ДНФ применяют различные методы.
1. Метод Блейка заключается в применении слева направо правила обобщенного склеивания  и правила поглощения
и правила поглощения  . На первом этапе применяется правило обобщенного склеивания до тех пор, пока это возможно, на втором – правило поглощения.
. На первом этапе применяется правило обобщенного склеивания до тех пор, пока это возможно, на втором – правило поглощения.
Пример.

После обобщенного склеивания получим
 .
.
После поглощения окончательно получим
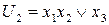 .
.
2. Метод Нельсона позволяет строить сокращенную ДНФ по заданной КНФ. На первом этапе в КНФ раскрываются скобки, на II – вычеркиваются буквы и конъюнкции с помощью правил:  ,
,  ,
,  .
.
Отметим, что при построении сокращенной ДНФ по методам 1 и 2 могут получиться ДНФ, имеющие большее число членов, чем исходная ДНФ.
3. При небольших значениях n можно использовать покрытие множества  в кубе
в кубе  на основе геометрического изображения гранями максимальной размерности. Для искомого построения в кубе
на основе геометрического изображения гранями максимальной размерности. Для искомого построения в кубе  отыскиваются грани максимальной размерности, содержащиеся в множестве
отыскиваются грани максимальной размерности, содержащиеся в множестве  , а затем составляется ДНФ из конъюнкций, соответствующих этим граням.
, а затем составляется ДНФ из конъюнкций, соответствующих этим граням.
Примеры. 2 примера.
4. Метод минимизирующих карт (карт Карно).
Наиболее простой (ручной) способ построения сокращенной ДНФ для функций небольшого числа переменных состоит в использовании минимизирующих карт, называемых картами Карно или диаграммами Вейча.
Он основан на задании функции прямоугольной таблицей, причем наборы значений переменных на каждой из сторон прямоугольника записываются в специальном виде (двоично-отраженные коды Грея).
Нахождение простых импликант сводится к выделению в таблице максимальных по включению прямоугольников, состоящих из единиц. Дополнительно полагается, что каждая клетка таблицы, примыкающая к одной из сторон прямоугольника, является соседней к клетке, примыкающей к противоположной стороне и расположенной на той же горизонтали или вертикали.
Например, функции  (1110 1101 1010 0000) соответствует карта Карно и множество
(1110 1101 1010 0000) соответствует карта Карно и множество  булева куба
булева куба  , показанные на рис.1
, показанные на рис.1

Рис. 1. Нахождение сокращенной ДНФ функции  .
.
Сокращенная ДНФ имеет следующий вид: 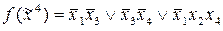 .
.
 2020-05-21
2020-05-21 130
130







