2020-05-21
292
ЛЕКЦИЯ № 11
Раздел 4. Колебания и волны
Колебания – это процесс, в котором какая-либо физическая величина повторяется с течением времени.
Если повторяемость осуществляется через равные промежутки времени, то колебания называются периодическими.
Минимальный промежуток времени, в течение которого совершается одно полное колебание, называется периодом.
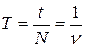
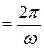, (11-1)
где n – линейная частота колебаний – количество колебаний за единицу времени, Гц;
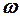– циклическая (круговая) частота колебаний – количество колебаний за 2 p сек, с-1.
Система, совершающая периодические колебания у положения равновесия, называется осциллятором.
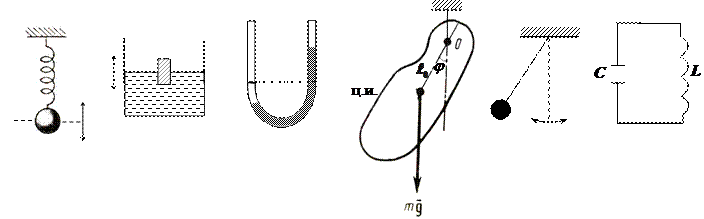Примеры осцилляторов:
Гл. 1. Колебания
Свободные (незатухающие) колебания осциллятора
Колебания осциллятора, происходящие в бездиссипативной среде (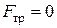
, R = 0), называются свободными (незатухающими) колебаниями.
- пружинный маятник
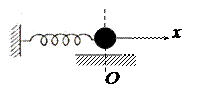
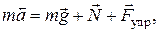
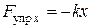
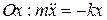
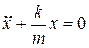(11-2)
- физический маятник
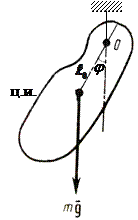
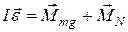
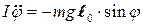
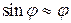
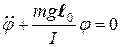(11-3)
- математический маятник
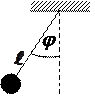
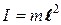
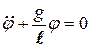(11-4)
- электрический колебательный контур
Заряженный конденсатор создает электрическое поле, которое обладает энергией. После подключения конденсатора к катушке начинается разряд конденсатора, в цепи появляется электрический ток, в катушке возникает магнитное поле. Т. к. сила тока в цепи будет изменяться, то изменяющееся магнитное поле согласно явлению самоиндукции приведет к возникновению электрических колебаний.
В таком осцилляторе (электрический колебательный контур) возникнут колебания заряда и напряжения на конденсаторе, силы тока в цепи, энергии электрического и магнитного полей.
 |
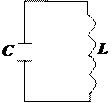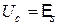
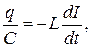
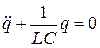(11-5)
Если обозначить коэффициент перед вторым слагаемым в уравнениях (11-2) – (11-5) через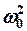 
и ввести обобщенную координату 
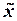, тогда дифференциальное уравнение любого осциллятора, совершающего свободные (незатухающие) колебания, примет вид:
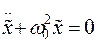(11-6)
Решением такого дифференциального уравнения является функция:
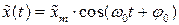или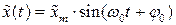 
(11-7)
где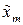 
= А – обобщенная амплитуда колебания – максимальное отклонение колеблющейся величины от положения равновесия;
j =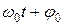 
- фаза колебания (
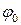- начальная фаза колебания).
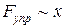
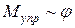
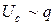
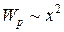
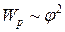
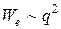
Колебания, происходящие по закону косинуса или синуса с постоянной амплитудой (у которых квазиупругая сила пропорциональна смещению в первой степени, а потенциальная энергия пропорциональна квадрату смещения), называются гармоническими.
Осциллятор – гармонический осциллятор.
Линейные гармонические колебания – колебания, у которых период колебания Т 0 не зависит от начальной амплитуды колебания.
Циклическая (круговая) частота и период свободных (незатухающих) линейных колебаний соответствующих гармонических осцилляторов вычисляют по формулам:
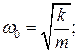
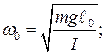
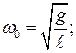
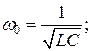(11-8)
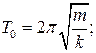
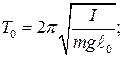
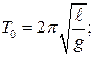
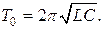(11-9)
