Прямых и плоскостей в пространстве

Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, описываются с помощью аксиом стереометрии.

Сформулируем три аксиомы о взаимном расположении точек, прямых и плоскостей в пространстве.

 

Аксиома 1 (А1). Через любые три точки, не лежащие на одно прямой, проходит плоскость, и притом только одна.

Если рассмотреть не три, а четыре точки, то эти четыре точки уже могут не лежать в одной плоскости.

 

Аксиома 2 (А2). Если две различные точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

В этом случае говорят, что прямая лежит в плоскости или плоскость проходит через прямую (например, для прямой а и плоскости ά этот факт записывается следующим образом: а ϵ ά).

 

Аксиома 3 (АЗ). Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

В этом случае говорят, что плоскости пересекаются по прямой (например, для плоскостей а и β, пересекающихся по прямой а, этот факт записывается следующим образом:   а ∩ β = а.

 

Отметим, что в пространстве существует бесконечное множество плоскостей и в каждой плоскости справедливы все аксиомы и теоремы планиметрии. Более того, все свойства и признаки, известные из курса планиметрии, справедливы для фигур, расположенных в разных плоскостях, то есть в пространстве.

 

Из приведенных выше аксиом вытекают два важнейших следствия:

 

Следствие 1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

 

Следствие 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.

 

Отметим также, при наличии каких обязательных элементов можно построить плоскость.

Итак, плоскость, и притом только одну, можно построить, если заданы следующие элементы:

 

· Три точки, не лежащие на одной прямой.

На Рис.а) показана плоскость ά, проходящая через точки А, В и С.

 

· Прямая и не лежащая на ней точка.

На Рис.б) показана плоскость ά, проходящая через точку А и прямую l.

 

· Две пересекающиеся прямые.

На Рис.в) показана плоскость ά, проходящая через пересекающиеся в точке М прямые а и b.

 

· Две параллельные прямые.

На Рис.г) показана плоскость ά, проходящая через параллельные прямые а и b.

 

Рис. а), б), в), г)

 

 

Вопрос 5. Решение задач

Задача 1.

Условие задачи:

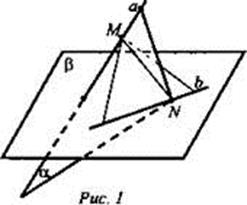
а и b - скрещивающиеся прямые;

γ – плоскость (проходит через прямую b и точку М), а ∉ γ, b ∈ γ.

Точка M ∈ а, точка N ∈ b.

Через а и N проведена плоскость α.

Через b и М проведена плоскость β (рис. 1).

Найти: а) лежит ли прямая b в плоскости α?

       б) пересекаются ли плоскости α и β?

 

 

Решение:

а) Если бы b ∈ α, тогда в плоскости α было бы две возможности:

1) b || а - но это противоречит условию;

2) b ∩ а - но это противоречит условию; b ∩ α в точке N, N ∉ а.

Вывод: b ∉ α.

 

б) 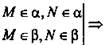прямая MN - общая для плоскостей α и β.

 

Вывод: α ∩ β по прямой MN.

Ответ: b ∉ α, MN - прямая, по которой α ∩ β.

 

 

ДОМАШНЕЕ ЗАДАНИЕ

 

Тесты: