Пример 1. Окружность с центром в начале координат задаётся уравнением х2+у2=R2
Тогда её часть расположенная выше оси абсцисс есть график функции 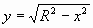 , где
, где 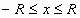 .
.
Используя геометрический смысл определённого интеграла площадь круга радиуса R
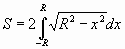 Вычислите этот интеграл.
Вычислите этот интеграл.
3. Объём тела вращения
| Пусть Г график непрерывной положительной функции у=f(x) в прямоугольной системе координат хОу. Необходимо вычислить объём тела вращения, ограниченного поверхностью вращения кривой Г вокруг оси х и плоскостями, проходящими через точки х = а, х = b перпендикулярно оси х. Если тело разбито на части как можно найти его объём? Объём тела равен сумме объёмов тел, его составляющих. Поэтому можно разбить наше тело на части. | 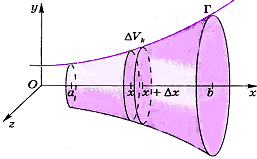
|
Разобьем отрезок [a;b] на части точками a<x0<x1<…..<xn<b. Рассмотрим цилиндр с высотой 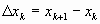 и радиуса основания yk = f(xk).
и радиуса основания yk = f(xk).
Как можно вычислить объём цилиндра? 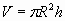
Тогда объем нашего цилиндра будет равен 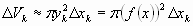
Тогда объём всего тела может быть записан при помощи приближённого равенства 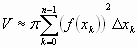 . Чтобы получить точное равенство надо взять предел
. Чтобы получить точное равенство надо взять предел 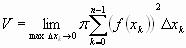
По определению определённого интеграла 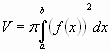 мы получили формулу для вычисления объёма тела вращения.
мы получили формулу для вычисления объёма тела вращения.
4. Решение задач
. Используя формулу объёма тела вращения, получите формулу для вычисления объёма конуса. 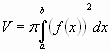
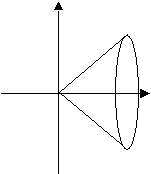
Чтобы воспользоваться полученной формулой необходимо задать с помощью функции прямую, которую будем вращать вокруг оси Ох.
Уравнение прямой y=kx 
k – угловой коэффициент прямой k=tg 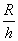
тогда уравнение прямой примет вид 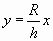 , а
, а 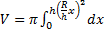 . найдите формулу объёма конуса.
. найдите формулу объёма конуса.
5. Вычислите объём тела, полученного вращением кривой – графика функции у= sinx, 0?х??, вокруг оси Ох.
- Найти объем тела, образованного вращением фигуры, ограниченной линиями (слайд 14)
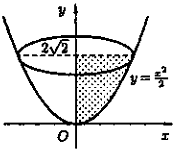
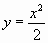 , х=0, у=
, х=0, у= 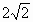 вокруг оси Оу
вокруг оси Оу
Решение:
Аналогично можно доказать, что объём тела, полученного вращением вокруг оси Оу можно вычислить по формуле 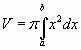
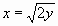
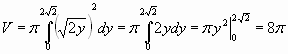
 2020-05-21
2020-05-21 152
152








