Алгебра 9 класс
Урок 16 – 18
Урок 16
369700
2000
1
1. Запишите десятичную дробь, равную сумме 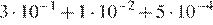 .
.
Решение.
Найдём сумму:
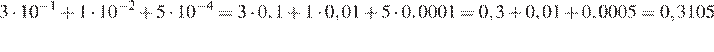
Ответ: 0,3105.
2. 203747
0,3105
Раздел кодификатора ФИПИ: 1.1 Действия с числами, сравнение чисел.
2. На координатной прямой отмечено число  Расположите в порядке убывания числа
Расположите в порядке убывания числа 
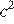 и
и 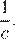
В ответе укажите номер правильного варианта.

1) 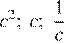
2) 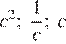
3) 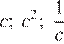
4) 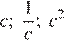
Решение.
Заметим, что 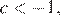 откуда следует, что
откуда следует, что 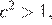
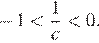 Таким образом,
Таким образом, 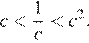
Правильный ответ указан под номером: 2.
3. 317600
2
Раздел кодификатора ФИПИ: 1.1 Действия с числами, сравнение чисел., 1.4 Точки на координатной прямой.
3. Найдите значение выражения 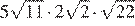 .
.
Решение.
Упростим выражение, разложив подкоренные выражения на множители и вынесем за знак корня полные квадраты чисел:
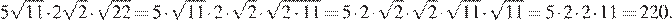
Ответ: 220.
4. 137285
220
Раздел кодификатора ФИПИ: 1.1 Действия с числами, сравнение чисел.
Решите систему уравнений 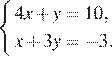
В ответе запишите сумму решений системы.
Решение.
Решим систему методом подстановки:
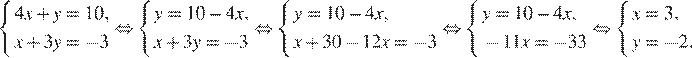
Ответ: 1.
5. 311370
1
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар.6)
Раздел кодификатора ФИПИ: 3.1 Решение уравнений и их систем.
На тарелке 12 пирожков: 5 с мясом, 4 с капустой и 3 с вишней. Наташа наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
Решение.
Вероятность того, что будет выбран пирожок с вишней равна отношению количества пирожков с вишней к общему количеству пирожков: 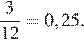
Ответ:0,25
132732
0,25
Раздел кодификатора ФИПИ: 6.5 Вероятности случайных событий.
6. Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) 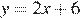
Б) 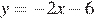
В) 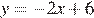
ГРАФИКИ
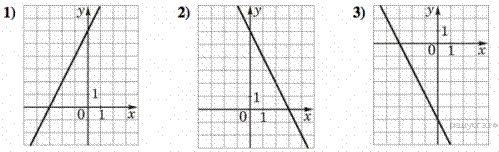
В таблице под каждой буквой укажите соответствующий номер.
Решение.
Напомним, что если прямая задана уравнением 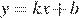 , то: при
, то: при 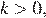 тангенс угла наклона прямой к оси абсцисс положителен.
тангенс угла наклона прямой к оси абсцисс положителен.
Уравнение 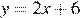 задает прямую, которая пересекает ось ординат в точке 6. Ее график изображен на рисунке 1).
задает прямую, которая пересекает ось ординат в точке 6. Ее график изображен на рисунке 1).
Уравнение 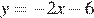 задает прямую, которая пересекает ось ординат в точке -6. Ее график изображен на рисунке 3).
задает прямую, которая пересекает ось ординат в точке -6. Ее график изображен на рисунке 3).
Уравнение 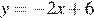 задает прямую, которая пересекает ось ординат в точке 6. Ее график изображен на рисунке 2).
задает прямую, которая пересекает ось ординат в точке 6. Ее график изображен на рисунке 2).
Тем самым, искомое соответствие: А — 1, Б — 3, В — 2.
Ответ: 132.
Урок 17
1. 351965
132
311910
27
Раздел кодификатора ФИПИ: 2.4 Преобразование рациональных выражений.
Площадь треугольника 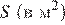 можно вычислить по формуле
можно вычислить по формуле 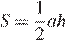 , где
, где 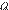 — сторона треугольника,
— сторона треугольника, 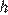 — высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону
— высота, проведенная к этой стороне (в метрах). Пользуясь этой формулой, найдите сторону 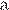 , если площадь треугольника равна
, если площадь треугольника равна 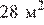 , а высота
, а высота 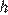 равна 14 м.
равна 14 м.
Решение.
Выразим сторону 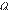 из формулы площади треугольника:
из формулы площади треугольника:
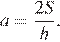
Подставляя, получаем:
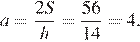
Ответ: 4.
311528
4
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 4)
 2020-05-21
2020-05-21 1160
1160







