Теорема Майергофера-Еругина

Пусть решение  уравнения

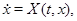
где функция  непрерывна для всех  и , определено на промежутке  и непродолжимо для значений .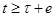

Тогда при 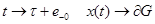, где  --- граница области .

Предположим теперь, что в окрестности любой точки 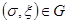 выполняются условия существования решения уравнения. Для простоты предположим, что  --- скаляр.