Рассмотрим систему

где  при
при  --- постоянные,
--- постоянные,  могут быть функциями координат, параметров и времени.
могут быть функциями координат, параметров и времени.
Определенно положительная функция

имеет производную в силу системы в следующем виде:

где

Таким образом,  будет определенно отрицательной или знакоотрицательной, если этим же свойством обладает форма
будет определенно отрицательной или знакоотрицательной, если этим же свойством обладает форма

Как известно, критерий Сильвестра легко переносится на случай квадратичных форм с переменными коэффициентами, и поэтому этот критерий с успехом может быть использован.
В качестве примера построим функцию Ляпунова для системы уравнений переходного процесса синхронного двигателя

Здесь  ,
,  --- постоянные,
--- постоянные,  --- возмущение рабочего угла,
--- возмущение рабочего угла,  --- возмущение силы тока, возникающее в результате наброса нагрузки на двигатель.
--- возмущение силы тока, возникающее в результате наброса нагрузки на двигатель.
В данном случае получаем

а в качестве матрицы  берем единичную матрицу. Таким образом, получим
берем единичную матрицу. Таким образом, получим

Построенная функция Ляпунова позволяет оценить область притяжения положения равновесия, что дает возможность быстро оценить допустимую предельную нагрузку на синхронный двигатель.
Предложенный метод в линейном случае дает необходимые и достаточные условия устойчивости, если найти подходящие выражения для  . Это следует из того, что всякая определенно положительная квадратичная форма линейным преобразованием может быть приведена к каноническому виду, т. е. к сумме квадратов переменных. Трудность этого метода состоит в подборе
. Это следует из того, что всякая определенно положительная квадратичная форма линейным преобразованием может быть приведена к каноническому виду, т. е. к сумме квадратов переменных. Трудность этого метода состоит в подборе  и матрицы
и матрицы  .
.
Метод Красовского
Исследуется система уравнений

Функция Ляпунова строится в виде  , где симметричная матрица
, где симметричная матрица  подбирается так, чтобы ее собственные числа были положительны и чтобы симметризованная матрица
подбирается так, чтобы ее собственные числа были положительны и чтобы симметризованная матрица

удовлетворяла критерию отрицательности Сильвестра. Имеем в силу системы

Таким образом, получим  и
и  .
.
В качестве примера рассмотрим уравнение

эквивалентное системе

Функцию Ляпунова выбираем в виде

Легко видеть, что

Очевидно, следует принять  и
и  , тогда будем иметь
, тогда будем иметь

и условие устойчивости в целом принимает вид  при любых
при любых  .
.
Метод Уокера-Кларка
Рассмотрим уравнение

эквивалентное системе

Функцию Ляпунова для системы предлагается брать в виде

где  специально подбирается с целью упрощения вида
специально подбирается с целью упрощения вида  и с целью выполнения неравенства
и с целью выполнения неравенства  .
.
Так, например, для системы

функцию  будем искать в виде
будем искать в виде

Имеем в силу системы

где

Очевидно, проще всего положить  ,
,  ,
,  , откуда
, откуда

и получаем функцию

В качестве второго примера рассмотрим уравнение

эквивалентное системе

Согласно предложенному способу следует принять

Имеем тогда

Если положить  , то условия устойчивости будут иметь вид
, то условия устойчивости будут иметь вид
 и
и  .
.
Но эти условия не могут быть удовлетворены для линейной функции
 .
.
Значительно полезней оказывается функция, предложенная Л. Америо,

В данном случае получим

и условия устойчивости в целом принимают вид
а)  при
при 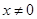 ,
,
б)  при
при  ,
,
в)  при
при 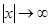 .
.
Градиентный метод
Предлагается начинать поиск функций Ляпунова с записи градиента этой функции в форме

где

Функции  подбираются из условия отрицательности
подбираются из условия отрицательности  и из требования, чтобы векторное поле
и из требования, чтобы векторное поле  было потенциальным. Это значит, что должны выполняться условия
было потенциальным. Это значит, что должны выполняться условия  . После того как найден градиент
. После того как найден градиент  сама функция
сама функция  определяется как криволинейный интеграл
определяется как криволинейный интеграл

В качестве примера рассмотрим уравнение

где  . Это уравнение эквивалентно системе
. Это уравнение эквивалентно системе

Будем искать вектор-градиент  в форме
в форме

В силу системы получим

Удобно положить  ,
,  ,
,  . Условия потенциальности поля дают
. Условия потенциальности поля дают  . Таким образом, имеем
. Таким образом, имеем  ,
,  ,
,  . Формула дает нам
. Формула дает нам

или, что то же самое,

Так как  , то условия устойчивости имеют вид
, то условия устойчивости имеют вид  и
и

 2020-05-21
2020-05-21 134
134








