2020-05-21
138
Пусть функция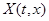 
уравнения определена и непрерывна для всех вещественных 
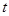и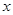 
как функция двух переменных.
Тогда любое решение уравнения неограниченно продолжим в обе стороны, если только выполнено неравенство
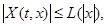
где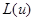 
--- функция, удовлетворяющая условию
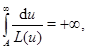
где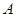 
--- число.
Доказательство проведем методом от противного.
Пусть существует решение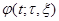 
, которое не является неограниченно продолжимым, например, вправо. Тогда на основании теоремы Майергофера-Еругина существует некоторое число 
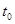такое, что 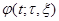принимает 
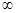разных знаков и при 
.
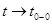Ввиду непрерывности решения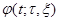 
как функции от 
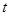оно должно бесконечное число раз проходить через нуль. А это означает, что существует последовательность значений 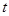, по которой это решение стремится к нулю. Это невозможно (по теореме Майергофера-Еругина).
Допустим, что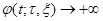 
при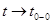 
. Так как 
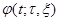--- решение уравнения, то 
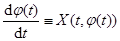в промежутке 
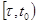. Допустим, что 
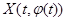не меняет знак. Тогда
|
|
|
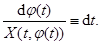
Проинтегрируем обе части по отрезку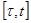 
, где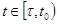 
получим
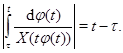
Произведем замену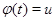 
. Получим
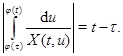
Тогда
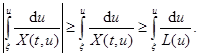
Таким образом получаем
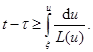
Теперь пусть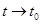 
. Учтем, что с заменой 
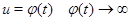и получаем
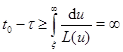
по условию теоремы. Это неравенство противоречиво, так как слева стоит конечная величина.
Рассмотрим общий случай, когда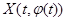 
может менять знак. Тогда
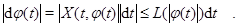
Так как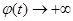 
при 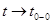, то с некоторого момента величина 
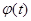станет положительной и знак модуля можно будет опустить. Тогда получим
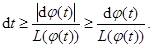
Проинтегрируем обе части от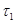 
до 
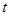, где 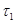--- значение, после которого 
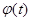становится положительным.
Сделаем замену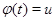 
, получим
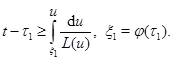
Устремим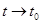 
и учтем
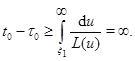
Последнее неравенство противоречиво, что говорит о том, что не существует решения, которое не является неограниченно продолжимым вправо.
Применение функций Ляпунова к исследованию продолжимости решений дифференциальных систем
