Пусть в 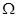 существует непрерывная вместе с частными производными первого порядка положительно определенная функция
существует непрерывная вместе с частными производными первого порядка положительно определенная функция 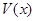 такая, что функция
такая, что функция 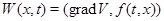 удовлетворяет неравенству
удовлетворяет неравенству
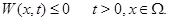
Тогда тривиальное решение системы устойчиво.
Теорема Вторая теорема Ляпунова
Пусть дополнительно к условиям первой теоремы для 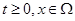 выполняется неравенство
выполняется неравенство 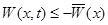 , где
, где 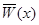 --- положительно определенная в
--- положительно определенная в 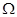 функция.
функция.
Тогда тривиальное решение системы асимптотически устойчиво.
Теорема Третья теорема Ляпунова
Пусть в 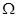 существует непрерывная вместе с частными производными первого порядка положительно определенная функция
существует непрерывная вместе с частными производными первого порядка положительно определенная функция 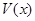 такая, что
такая, что
а) 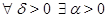 и
и 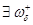
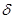 -окрестность точки
-окрестность точки 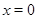 , в которой выполняется неравенство
, в которой выполняется неравенство 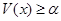 ;
;
б) 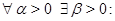 из
из 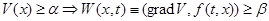 , справедливое при всех
, справедливое при всех 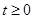 .
.
Тогда тривиальное решение системы неустойчиво.
Замечание. Недостаток изложенных методов заключается в том, что не существует достаточно общего конструктивного способа построения функций 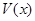 .
.
Замечание. Горбунов показал, что для линейных систем с непрерывными коэффициентами функция Ляпунова всегда существует в виде квадратичной формы.
Замечание. Для дифференциальных уравнений, описывающих некоторые механические системы, роль функции Ляпунова играет потенциальная энергия 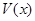 . Сама система имеет вид
. Сама система имеет вид 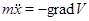 , а соответствующая функция
, а соответствующая функция 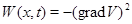 .
.
В замечании было обращено внимание на отсутствие общей методики построения функций Ляпунова для конкретных дифференциальных систем. Ниже приведены некоторые известные способы построения функций Ляпунова.
Методы построения функций Ляпунова
Энергетический метод
Применяется для системы второго порядка.
Рассмотрим систему
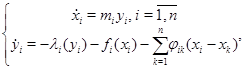
где 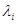 ,
, 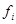 ,
, 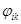 непрерывны,
непрерывны, 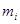 --- положительные постоянные и
--- положительные постоянные и 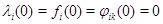 ,
, 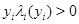 при
при 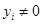 ,
, 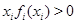 при
при 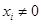 ,
, 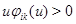 при
при 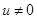 , где
, где 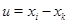 ,
, 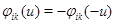 ,
, 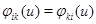 .
.
В качестве механической модели можно взять движение системы 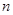 материальных точек
материальных точек 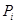 с массой
с массой 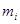 , в которой точка
, в которой точка 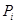 подвергается действию сил
подвергается действию сил 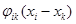 , выражающие влияние других точек
, выражающие влияние других точек 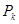 этой системы на точку
этой системы на точку 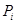 .
.
Тогда можно дать механическую интерпретацию. Функцию 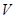 составим как полную энергию системы, то есть как сумму кинетической и потенциальной энергий. Получим
составим как полную энергию системы, то есть как сумму кинетической и потенциальной энергий. Получим
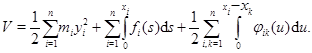
Очевидно, что эта функция определенно положительная.
Найдем производную функции 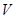 в силу системы, получим
в силу системы, получим
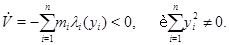
Так как члены 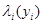 определяют силы, способствующие рассеиванию механической энергии, то полная энергия системы убывает, а значит, соображений производная знакоотрицательная.
определяют силы, способствующие рассеиванию механической энергии, то полная энергия системы убывает, а значит, соображений производная знакоотрицательная.
Метод Малкина
Рассмотрим уравнение
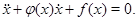
Это уравнение эквивалентно системе
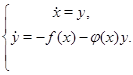
Соответствующая линейная система имеет вид
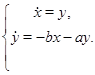
Для нее может быть построена функция Ляпунова
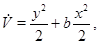
причем 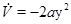 .
.
Замечаем теперь, что 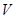 не содержит в своей записи параметра
не содержит в своей записи параметра 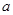 , поэтому эта же функция пригодна для исследования системы
, поэтому эта же функция пригодна для исследования системы
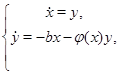
но непригодна для системы.
Чтобы получить функцию Ляпунова для системы, необходимо найти аналог члена 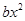 в записи
в записи 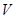 . Но с точки зрения механики величина
. Но с точки зрения механики величина 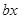 (или
(или 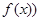 характеризует восстанавливающую силу, а величина
характеризует восстанавливающую силу, а величина 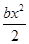 соответствует потенциальной энергии. Поэтому естественно принять за функцию Ляпунова для системы функцию
соответствует потенциальной энергии. Поэтому естественно принять за функцию Ляпунова для системы функцию
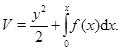
Очевидно, получим в силу системы
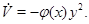
Условия устойчивости в целом запишутся следующим образом:
а) 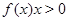 при
при 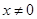 ,
,
б) 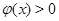 ,
,
в) 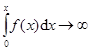 при
при 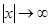 .
.
Легко проверить, что множество 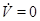 , то есть прямая
, то есть прямая 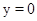 не содержит целых траекторий, кроме начала координат.
не содержит целых траекторий, кроме начала координат.
Укажем другой подход к задаче. Производя в уравнении замену переменной 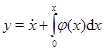 получим систему
получим систему
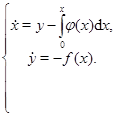
Используя снова прежнюю функцию Ляпунова, получим в силу системы
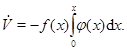
Условия устойчивости в целом в данном случае улучшаются, так как условие б) заменяется менее ограничительным условием
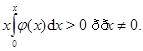
 2020-05-21
2020-05-21 148
148








