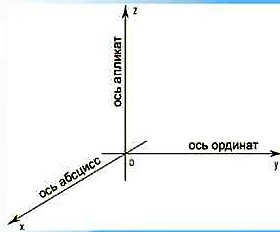
 Три попарно перпендикулярные прямые, на которых выбрано направление и единичные отрезки, называются прямоугольной системой координат в пространстве.
Три попарно перпендикулярные прямые, на которых выбрано направление и единичные отрезки, называются прямоугольной системой координат в пространстве.
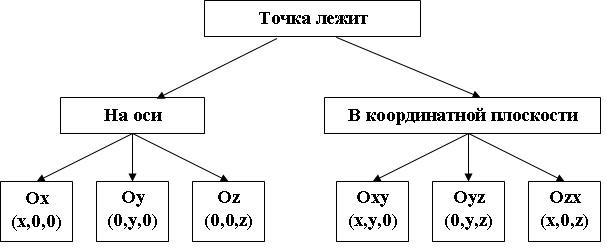
Прямые с выбранными на них направлениями называются осями координат, а их общая точка – началом координат. Она обозначается буквой О. Оси координат обозначаются так: Ох, Оу. Их называют: ось абсцисс, ось ординат, ось аппликат. Вся система обозначается Охуz.
Три плоскости, проходящие соответственно через оси координат Ох и Оу, Оу и Оz, Оz и Ох - координатные плоскости. Их обозначают Оху, Оуz, Оzх.
Точка О разделяет каждую из осей координат на 2 луча, один из них – положительная полуось, другой – отрицательная полуось.
В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел, которые называются её координатами.
М (х; у; z), х – абсцисса, у – ордината, z- аппликата.
При решении задач в координатах применяют правила:
1. Если вектор 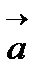 имеет координаты
имеет координаты 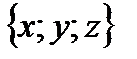 , то его можно разложить по координатным векторам
, то его можно разложить по координатным векторам
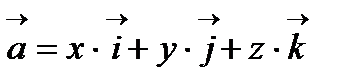 где
где 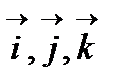 - координатные (базисные) векторы.
- координатные (базисные) векторы.
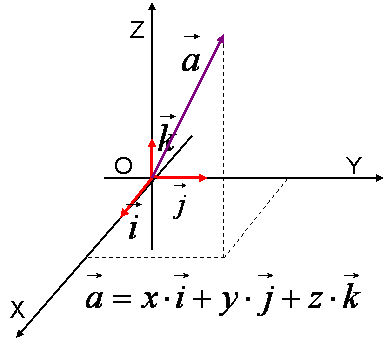
Базисные векторы записываются следующим образом:
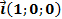
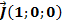

Пусть даны векторы 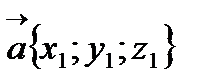 и
и 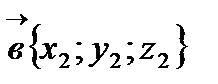
2. Если 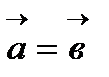 , то
, то 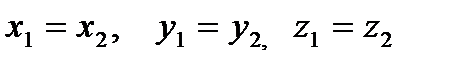
3. 
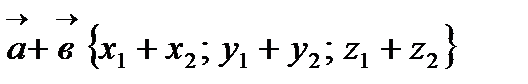
4. 
5. 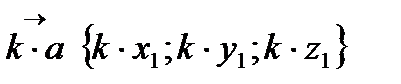
Скалярное произведение векторов: 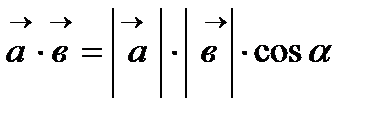
Скалярное произведение векторов в координатах: 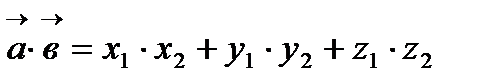
6. Признаки ортогональности и коллинеарности векторов.
1) 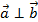 , если
, если 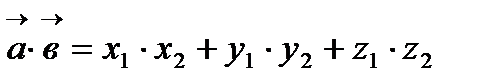 = 0 {векторы перпендикулярны (ортогональны), если их скалярное произведение (сумма произведений одноименных координат) равно нулю}.
= 0 {векторы перпендикулярны (ортогональны), если их скалярное произведение (сумма произведений одноименных координат) равно нулю}.
2) 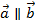 , векторы параллельны(коллинеарные) если координаты векторов пропорциональны
, векторы параллельны(коллинеарные) если координаты векторов пропорциональны
Пусть даны векторы 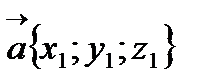 и
и 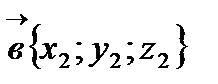 , если
, если 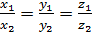 .
.
Вычисление координат середины отрезка

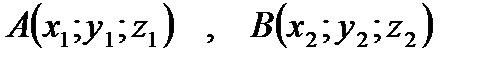 и
и 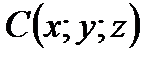 - середина отрезка
- середина отрезка
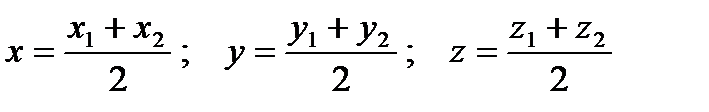
Вычисление длины вектора по его координатам

Расстояние между двумя точками
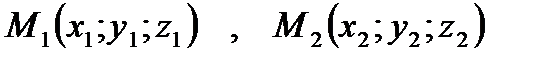
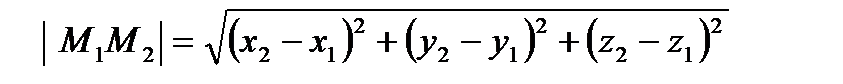
Угол между векторами 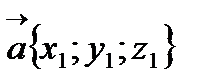 и
и 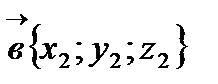
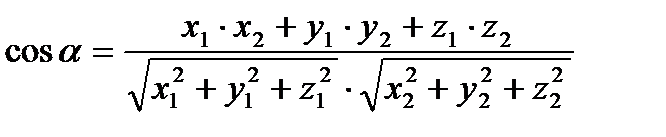
Угол между прямыми, где 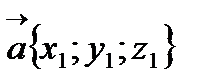 и
и 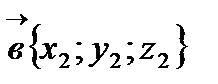 - направляющие векторы прямых
- направляющие векторы прямых
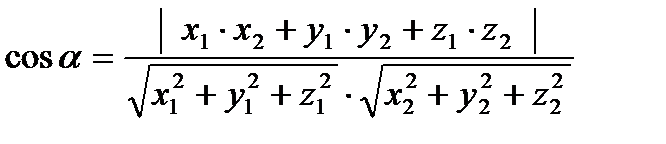


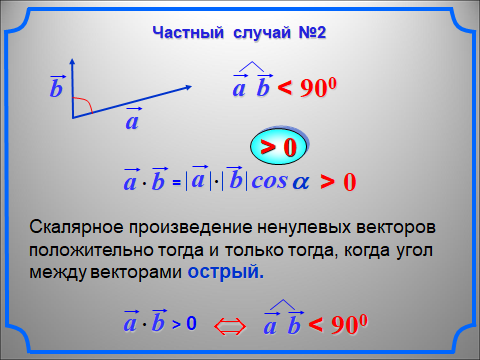
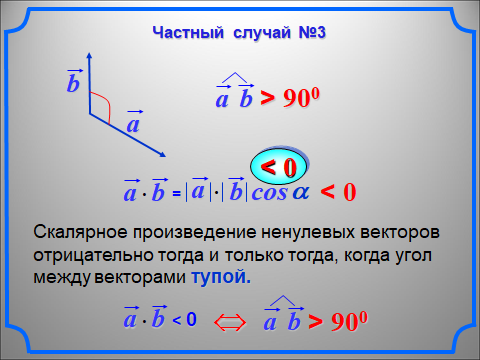

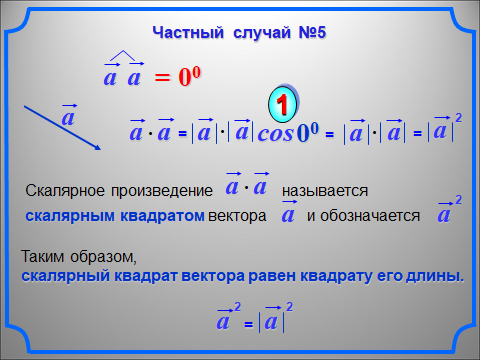
Примеры решения задач:
№1
Дано: 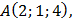
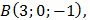
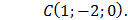
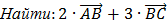
Решение
1) Находим координаты вектора 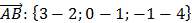
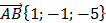 ;
;
2) Затем находим координаты вектора 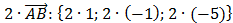
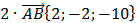
3) Теперь находим аналогично координаты вектора 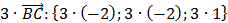

4) Теперь находим сумму данных векторов, складывая соответствующие координаты: 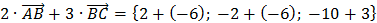
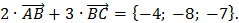
Ответ: 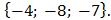
№ 2
Дано: 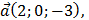
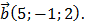
 ; 2)
; 2) 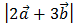 .
.
Решение
1.
1) Находим координаты вектора 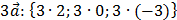
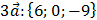 ;
;
2) Затем находим разность векторов 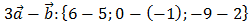
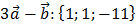 ;
;
3) Теперь находим длину вектора 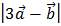 :
: 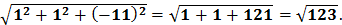
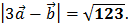
2.
1) Находим координаты вектора 
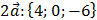 ;
;
2) Находим координаты вектора 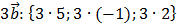
 ;
;
3) Затем находим сумму векторов 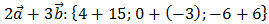
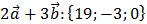 ;
;
4) Теперь находим длину вектора 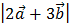 :
: 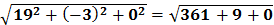

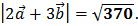
Ответ: 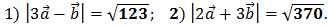
ВАРИАНТ
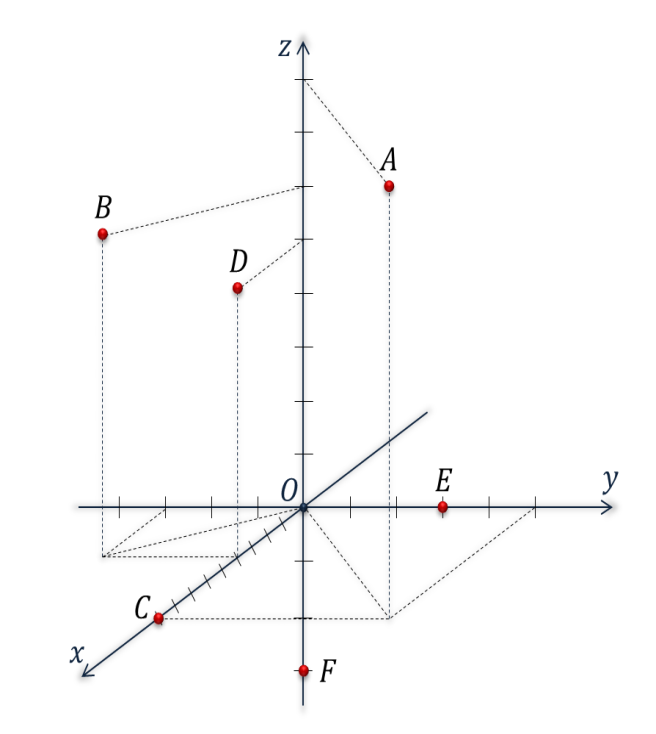
1. По данным рисунка определите координаты всех точек.
2. Найдите длины векторов: АВ, BD, DC,CF, FE, DA.
3. Найдите скалярное произведение векторов: AB и CF, FE и DA.
4. Вычислите угол между векторами BD и DC.
_______________________________________________________________________
ВАРИАНТ
1. По данным рисунка определите координаты всех точек.
2. Найдите длины векторов: ВC, DF, DE, BF, AE, CE.
3. Найдите скалярное произведение векторов: DF и AE; BF и DE.
4. Вычислите угол между векторами BC и CE.

Домашнее задание
«Метод координат в пространстве»
Вариант 1
1.Даны точки А(5; 0; 2), В(4; -3; 2),
С(0; 0; 1), D(2; -4; -4). Найдите:
а) координаты векторов 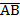 и и 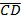 ;
б) координаты векторов ;
б) координаты векторов 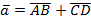 ; ; 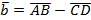 ; ; 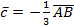 .
в) длины векторов .
в) длины векторов 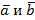 ;
г) скалярное произведение векторов ;
г) скалярное произведение векторов 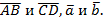 2. Вершины треугольника КМN имеют координаты K(-2; 3; -2), M(8; 1;2), N(2; -3; 0). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
2. Вершины треугольника КМN имеют координаты K(-2; 3; -2), M(8; 1;2), N(2; -3; 0). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
| Домашнее задание
«Метод координат в пространстве»
Вариант 2
1.Даны точки А(5; -5; 0), В(-2; 1; -3),
С(0; 3; 1), D(1; 3; -4). Найдите:
а) координаты векторов 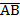 и и 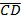 ;
б) координаты векторов ;
б) координаты векторов 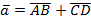 ; ; 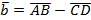 ; ; 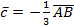 .
в) длины векторов .
в) длины векторов 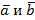 ;
г) скалярное произведение векторов ;
г) скалярное произведение векторов 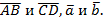 2. Вершины треугольника КМN имеют координаты K(8; 3; 5), M(14; 1;0), N(12; -5; 0). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
2. Вершины треугольника КМN имеют координаты K(8; 3; 5), M(14; 1;0), N(12; -5; 0). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
|
Домашнее задание
«Метод координат в пространстве»
Вариант 3
1.Даны точки А(4; 4; 0), В(1; 0; 5),
С(-1; -5; 0), D(10; -1; 0). Найдите:
а) координаты векторов 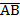 и и 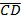 ;
б) координаты векторов ;
б) координаты векторов 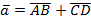 ; ; 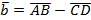 ; ; 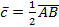 .
в) длины векторов .
в) длины векторов 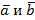 ;
г) скалярное произведение векторов ;
г) скалярное произведение векторов 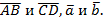 2. Вершины треугольника КМN имеют координаты K(3; 8; -4), M(-5; 8;4), N(-5; 0;-4). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
2. Вершины треугольника КМN имеют координаты K(3; 8; -4), M(-5; 8;4), N(-5; 0;-4). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
| Домашнее задание
«Метод координат в пространстве»
Вариант 4
1.Даны точки А(3; 0; 3), В(0; -3; 1),
С(-1; 2; 1), D(4; 4; -2). Найдите:
а) координаты векторов 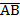 и и 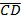 ;
б) координаты векторов ;
б) координаты векторов 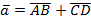 ; ; 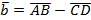 ; ; 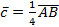 .
в) длины векторов .
в) длины векторов 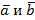 ;
г) скалярное произведение векторов ;
г) скалярное произведение векторов 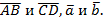 2. Вершины треугольника КМN имеют координаты K(5; -1; -3), M(1; 6;2), N(9; 6; 2). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
2. Вершины треугольника КМN имеют координаты K(5; -1; -3), M(1; 6;2), N(9; 6; 2). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
|
Домашнее задание
«Метод координат в пространстве»
Вариант 5
1.Даны точки А(-1; -2; -1), В(3; -2; 0),
С(4; -4; 0), D(0; 3; 2). Найдите:
а) координаты векторов 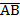 и и 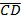 ;
б) координаты векторов ;
б) координаты векторов 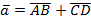 ; ; 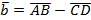 ; ; 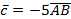 .
в) длины векторов .
в) длины векторов 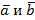 ;
г) скалярное произведение векторов ;
г) скалярное произведение векторов 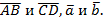 2. Вершины треугольника КМN имеют координаты K(4; 5; -3), M(6; 13;0),N(-4; 7; 0). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
2. Вершины треугольника КМN имеют координаты K(4; 5; -3), M(6; 13;0),N(-4; 7; 0). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
| Домашнее задание
«Метод координат в пространстве»
Вариант 6
1.Даны точки А(3; 3; 1), В(-3; 1; -3),
С(0; -2; 5), D(2; 3; 4). Найдите:
а) координаты векторов 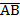 и и 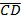 ;
б) координаты векторов ;
б) координаты векторов 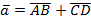 ; ; 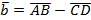 ; ; 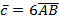 .
в) длины векторов .
в) длины векторов 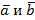 ;
г) скалярное произведение векторов ;
г) скалярное произведение векторов 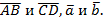 2. Вершины треугольника КМN имеют координаты K(4; -3; 5), M(7;-12;0), N(-1; -7; 2). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
2. Вершины треугольника КМN имеют координаты K(4; -3; 5), M(7;-12;0), N(-1; -7; 2). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
|
Домашнее задание
«Метод координат в пространстве»
Вариант 7
1.Даны точки А(1; -2; 0), В(2; 2; 3),
С(3; 0; 5), D(-4; -1; -2). Найдите:
а) координаты векторов 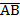 и и 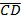 ;
б) координаты векторов ;
б) координаты векторов 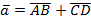 ; ; 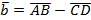 ; ; 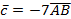 .
в) длины векторов .
в) длины векторов 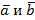 ;
г) скалярное произведение векторов ;
г) скалярное произведение векторов 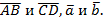 2. Вершины треугольника КМN имеют координаты K(-2; 0; 4), M(8; -2; 4), N(6; 8; 4). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
2. Вершины треугольника КМN имеют координаты K(-2; 0; 4), M(8; -2; 4), N(6; 8; 4). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
| Домашнее задание
«Метод координат в пространстве»
Вариант 8
1.Даны точки А(-3; 1; 0), В(0; 0; 1),
С(2; -2; 2), D(-1; -1; -4). Найдите:
а) координаты векторов 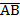 и и 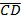 ;
б) координаты векторов ;
б) координаты векторов 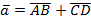 ; ; 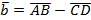 ; ; 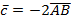 .
в) длины векторов .
в) длины векторов 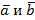 ;
г) скалярное произведение векторов ;
г) скалярное произведение векторов 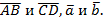 2. Вершины треугольника КМN имеют координаты K(8;7;-3), M(10;15;-3),N(2;13;-3). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
2. Вершины треугольника КМN имеют координаты K(8;7;-3), M(10;15;-3),N(2;13;-3). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
|
Домашнее задание
«Метод координат в пространстве»
Вариант 9
1.Даны точки А(3; 0; 2), В(-1; -2; 4),
С(0; 0; 2), D(-3; 3; 2). Найдите:
а) координаты векторов 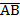 и и 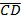 ;
б) координаты векторов ;
б) координаты векторов 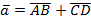 ; ; 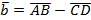 ; ; 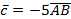 .
в) длины векторов .
в) длины векторов 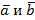 ;
г) скалярное произведение векторов ;
г) скалярное произведение векторов 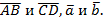 2. Вершины треугольника КМN имеют координаты K(8; 3; 4), M(14; 1;0), N(12;-5;-4). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
2. Вершины треугольника КМN имеют координаты K(8; 3; 4), M(14; 1;0), N(12;-5;-4). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
| Домашнее задание
«Метод координат в пространстве»
Вариант 10
1.Даны точки А(0; -2; 1), В(-2; -2; 0),
С(1; 2; 3), D(1; 0; -1). Найдите:
а) координаты векторов 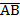 и и 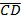 ;
б) координаты векторов ;
б) координаты векторов 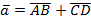 ; ; 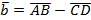 ; ; 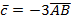 .
в) длины векторов .
в) длины векторов 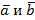 ;
г) скалярное произведение векторов ;
г) скалярное произведение векторов 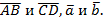 2. Вершины треугольника КМN имеют координаты K(0; -2; 5), M(-2;8;-1), N(8; 6; 4). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
2. Вершины треугольника КМN имеют координаты K(0; -2; 5), M(-2;8;-1), N(8; 6; 4). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
|
Домашнее задание
«Метод координат в пространстве»
Вариант 11
1.Даны точки А(-2; 0; 3), В(1; 1; 1),
С(3; -2; -2), D(1; 2; 0). Найдите:
а) координаты векторов 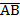 и и 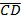 ;
б) координаты векторов ;
б) координаты векторов 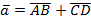 ; ; 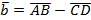 ; ;  .
в) длины векторов .
в) длины векторов 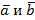 ;
г) скалярное произведение векторов ;
г) скалярное произведение векторов 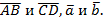 2. Вершины треугольника КМN имеют координаты K(3; 8; 3), M(8; 14; 1), N(6;12;-5). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
2. Вершины треугольника КМN имеют координаты K(3; 8; 3), M(8; 14; 1), N(6;12;-5). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
| Домашнее задание
«Метод координат в пространстве»
Вариант 12
1.Даны точки А(-1; 2; -2), В(3; -3; 0),
С(0; 1; -1), D(-2; 3; 1). Найдите:
а) координаты векторов 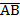 и и 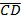 ;
б) координаты векторов ;
б) координаты векторов 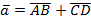 ; ; 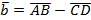 ; ; 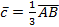 .
в) длины векторов .
в) длины векторов 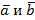 ;
г) скалярное произведение векторов ;
г) скалярное произведение векторов 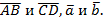 2. Вершины треугольника КМN имеют координаты K(2;-2; 3), M(2; 8; 1), N(2; 2;-3). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
2. Вершины треугольника КМN имеют координаты K(2;-2; 3), M(2; 8; 1), N(2; 2;-3). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой)
|
 2020-05-25
2020-05-25 493
493







