Теорема 8.2.1. Пусть язык 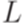 является контекстно-свободным. Тогда язык
является контекстно-свободным. Тогда язык 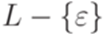 порождается некоторой контекстно-свободной грамматикой без
порождается некоторой контекстно-свободной грамматикой без 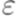 - правил.
- правил.
Доказательство. Пусть дана контекстно-свободная грамматика 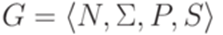 , порождающая язык L. Проведем серию преобразований множества P.
, порождающая язык L. Проведем серию преобразований множества P.
Если для каких-то 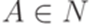 ,
, 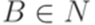 ,
, 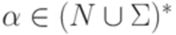 и
и 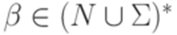 множество P содержит правила
множество P содержит правила 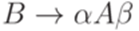 и
и 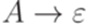 , но не содержит правила
, но не содержит правила 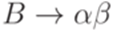 , то добавим это правило в P. Повторяем эту процедуру, пока возможно.
, то добавим это правило в P. Повторяем эту процедуру, пока возможно.
Теперь исключим из множества P все правила вида 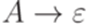 . Полученная грамматика порождает язык
. Полученная грамматика порождает язык 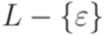 .
.
Пример 8.2.2. Рассмотрим язык L, порождаемый грамматикой
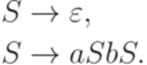
Язык 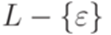 порождается грамматикой
порождается грамматикой
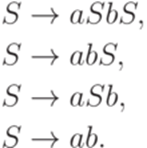
 2020-05-25
2020-05-25 189
189








